Проекции. Геометрическая операция проектирования (проецирования) выполняет отображение объектов на картинной плоскости

Геометрическая операция проектирования (проецирования) выполняет отображение объектов на картинной плоскости. При этом через каждую точку объекта проводятся прямые, начинающиеся в некотором центре. Точки пересечения этих прямых с плоскостью изображения образуют проекцию.

Различают проектирование параллельное и центральное. При центральном проектировании все прямые исходят из одной точки - центра пучка. К центральным относятся перспективные проекции (прямая - обычная и обратная - иконы). При параллельном проектировании центр пуч-

ка находится в бесконечности. Каждый из двух

основных классов разбивается на несколько под-

классов в зависимости от взаимного расположе-

ния картинной плоскости и координатных осей.

КЛАССИФИКАЦИЯ ПРОЕКЦИЙ

z z При ортографической проекции картинная плос-

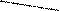
кость совпадает с одной из координатных плос-

y костей или параллельна ей. Матрица проектиро-

x x y вания вдоль оси х на плоскость yz имеет вид:

.

Если плоскость проектирования параллельна координатной плоскости, матрица умножается на матрицу сдвига: .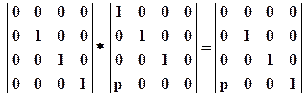

Матрицы для других осей координат: ; .

При аксонометрической проекции проектирующие прямые перпендикулярны плоскости отображения. Аксонометрия - от греческого axon - ось + метрия - изображение. Предмет вместе со связанной с ним системой координат проектируется на некоторую плоскость. В соответствии с взаимным расположением плоскости проектирования и координатных осей различают проекции:

· триметрию (плоскость находится относительно осей координат под различными углами для каждой оси) - используется редко;

· диметрию (два из трех углов между осями и плоскостью равны, т.е. две оси одинаково сокращены);

· изометрию (все углы равны, т.е. масштаб по всем осям одинаков).

Каждая из этих проекций получается комбинацией поворотов,

после чего следует параллельное (ортографическое) проекти-

рование. Можно вывести соответствующие матрицы, некото-

рые подходы обозначены в [ 1 ].

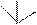Изометрия Диметрия

Косоугольные проекции используют пучок прямых, не перпендикулярных плоскости отображения. Выделяют два вида косоугольных проекций:

· свободную (угол наклона проектирующих прямых к плоскости отображения равен );

· кабинетную (частный случай свободной, масштаб по третьей оси в 2 раза меньше).

Все это также представимо в матричном виде. Так, при проектировании на плоскость xy точки с координатами x=0, y=0, z=1 имеем . Вид матрицы:.

Для свободной проекции . Для кабинетной проекции .

Перспективные (центральные) проекции более сложны. Они получаются путем перспективного преобразования и проектирования на некоторую плоскость наблюдения. Вводятся параметры, описывающие центр проектирования, т.е. точку, откуда "смотрят" на объект. Пусть эта точка имеет координаты . Тогда матрица перспективного преобразования в пространстве имеет вид: 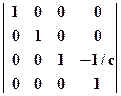. Выкладки получения приведены в [ 1,8 ]. Член матрицы, характеризующий местоположение центра проектирования, выводится из уравнения прямой, проведенной из центра проектирования в некоторую точку объекта. Если мы хотим, например, плоскость наблюдения совместить с плоскостью xy, матрица примет вид: . Нулевое значение в третьем столбце третьей строки отражает факт .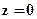

В общем случае при нахождении центра проектирования на осях z или y или x матрицы преобразования будут иметь соответственно вид: , , 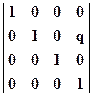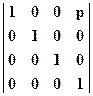. Это матрицы одноточечных преобразований.

Пример - преобразование единичного куба, центр проектирования лежит на оси z.

Если 2 элемента в четвертом столбце матрицы ненулевые (последнюю строку 0 0 0 1 не считаем), получается двухточечная или угловая перспектива, 3 элемента ненулевые - трехточечная или косая перспектива. Углы наклона определяются координатами центра проектирования. Для 2- и 3-точечных проекций оси координат системы не параллельны плоскости отображения.

C`D`

y`

C`

G` I` 2-x точечная перспектива D` G` 3-x точечная перспектива

I`

Для произвольного центра проектирования с координатами 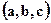матрица преобразования: .

Из школьного курса черчения и курса начертательной геометрии известно, что по нескольким проекциям можно восстановить изображение. Для компьютерной графики это соответствует обратным матричным преобразованиям. Т.к. для восстановления изображения используются несколько проекций, преобразования весьма сложны и длительны. Этим объясняется высокая ресурсоемкость подобных задач.

Как все это реализовать (запрограммировать)? Здесь удобно использовать объектно-ориентированный подход. Фактически, мы работаем с векторами, т.к. координаты точки - 3 числа. Для класса ВЕКТОР (vector) можно определить систему операций (например, поэлементное сложение и вычитание векторов и т.д.). Определяются также основные функции. Аналогично вводится класс МАТРИЦА (matrix). Примеры программ [ 1 ]:

#include <math.h>

#include "Matrix.h"

Matrix:: Matrix (double v)

{

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

x [i][j] = (i == j)? v: 0.0;

x [3][3] = 1;

}

void Matrix:: Invert ()

{

Matrix Out (1);

for (int i = 0; i < 4; i++)

{

double d = x [i][i];

if (d!= 1.0)

{

for (int j = 0; j < 4; j++)

{

Out.x [i][j] /= d;

x [i][j] /= d;

}

}

for (int j = 0; j < 4; j++)

{

if (j!= i)

{

if (x [j][i]!= 0.0)

{

double mulby = x[j][i];

for (int k = 0; k < 4; k++)

{

x [j][k] -= mulby * x [i][k];

Out.x [j][k] -= mulby * Out.x [i][k];

}

}

}

}

}

*this = Out;

}

void Matrix:: Transpose ()

{

double t;

for (int i = 0; i < 4; i++)

for (int j = i; j < 4; j++)

if (i!= j)

{

t = x [i][j];

x [i][j] = x [j][i];

x [j][i] = t;

}

}

Matrix& Matrix:: operator += (const Matrix& A)

{

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

x [i][j] += A.x [i][j];

return *this;

}

Matrix& Matrix:: operator -= (const Matrix& A)

{

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

x [i][j] -= A.x [i][j];

return *this;

}

Matrix& Matrix:: operator *= (double v)

{

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

x [i][j] *= v;

return *this;

}

Matrix& Matrix:: operator *= (const Matrix& A)

{

Matrix res = *this;

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

{

double sum = 0;

for (int k = 0; k < 4; k++)

sum += res.x [i][k] * A.x [k][j];

x [i][j] = sum;

}

return *this;

}

Matrix operator + (const Matrix& A, const Matrix& B)

{

Matrix res;

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

res.x [i][j] = A.x [i][j] + B.x [i][j];

return res;

}

Matrix operator - (const Matrix& A, const Matrix& B)

{

Matrix res;

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

res.x [i][j] = A.x [i][j] - B.x [i][j];

return res;

}

Matrix operator * (const Matrix& A, const Matrix& B)

{

Matrix res;

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

{

double sum = 0;

for (int k = 0; k < 4; k++)

sum += A.x [i][k] * B.x [k][j];

res.x [i][j] = sum;

}

return res;

}

Matrix operator * (const Matrix& A, double v)

{

Matrix res;

for (int i = 0; i < 4; i++)

for (int j = 0; j < 4; j++)

res.x [i][j] = A.x [i][j] * v;

return res;

}

Vector operator * (const Matrix& M, const Vector& v)

{

Vector res;

res.x = v.x * M.x[0][0] + v.y * M.x[1][0] + v.z * M.x[2][0] + M.x[3][0];

res.y = v.x * M.x[0][1] + v.y * M.x[1][1] + v.z * M.x[2][1] + M.x[3][1];

res.z = v.x * M.x[0][2] + v.y * M.x[1][2] + v.z * M.x[2][2] + M.x[3][2];

double denom = v.x * M.x[0][3] + v.y * M.x[1][3] + v.z * M.x[2][3] +

M.x[3][3];

if (denom!= 1.0)

res /= denom;

return res;

}

//////////////////////// Derived classes /////////////////////////////

Matrix Translate (const Vector& Loc)

{

Matrix res (1);

res.x [3][0] = Loc.x;

res.x [3][1] = Loc.y;

res.x [3][2] = Loc.z;

return res;

}

Matrix Scale (const Vector& v)

{

Matrix res (1);

res.x [0][0] = v.x;

res.x [1][1] = v.y;

res.x [2][2] = v.z;

return res;

}

Matrix RotateX (double Angle)

{

Matrix res (1);

double Cosine = cos (Angle);

double Sine = sin (Angle);

res.x [1][1] = Cosine;

res.x [2][1] = -Sine;

res.x [1][2] = Sine;

res.x [2][2] = Cosine;

return res;

}

Matrix RotateY (double Angle)

{

Matrix res (1);

double Cosine = cos (Angle);

double Sine = sin (Angle);

res.x [0][0] = Cosine;

res.x [2][0] = -Sine;

res.x [0][2] = Sine;

res.x [2][2] = Cosine;

return res;

}

Matrix RotateZ (double Angle)

{

Matrix res (1);

double Cosine = cos (Angle);

double Sine = sin (Angle);

res.x [0][0] = Cosine;

res.x [1][0] = -Sine;

res.x [0][1] = Sine;

res.x [1][1] = Cosine;

return res;

}

Matrix Rotation (const Vector& axis, double angle)

{

Matrix res (1);

double Cosine = cos (angle);

double Sine = sin (angle);

res.x [0][0] = axis.x * axis.x + (1 - axis.x * axis.x) * Cosine;

res.x [0][1] = axis.x * axis.y * (1 - Cosine) + axis.z * Sine;

res.x [0][2] = axis.x * axis.z * (1 - Cosine) - axis.y * Sine;

res.x [0][3] = 0;

res.x [1][0] = axis.x * axis.y * (1 - Cosine) - axis.z * Sine;

res.x [1][1] = axis.y * axis.y + (1 - axis.y * axis.y) * Cosine;

res.x [1][2] = axis.y * axis.z * (1 - Cosine) + axis.x * Sine;

res.x [1][3] = 0;

res.x [2][0] = axis.x * axis.z * (1 - Cosine) + axis.y * Sine;

res.x [2][1] = axis.y * axis.z * (1 - Cosine) - axis.x * Sine;

res.x [2][2] = axis.z * axis.z + (1 - axis.z * axis.z) * Cosine;

res.x [2][3] = 0;

res.x [3][0] = 0;

res.x [3][1] = 0;

res.x [3][2] = 0;

res.x [3][3] = 1;

return res;

}

Matrix MirrorX ()

{

Matrix res (1);

res.x [0][0] = -1;

return res;

}

Matrix MirrorY ()

{

Matrix res (1);

res.x [1][1] = -1;

return res;

}

Matrix MirrorZ ()

{

Matrix res (1);

res.x [2][2] = -1;

return res;

}

/********************************************************************************/

#ifndef __MATRIX__

#define __MATRIX__

#include "Vector.h"

class Matrix

{

public:

double x [4][4];

Matrix () {};

Matrix (double);

Matrix& operator += (const Matrix&);

Matrix& operator -= (const Matrix&);

Matrix& operator *= (const Matrix&);

Matrix& operator *= (double);

Matrix& operator /= (double);

void Invert ();

void Transpose ();

friend Matrix operator + (const Matrix&, const Matrix&);

friend Matrix operator - (const Matrix&, const Matrix&);

friend Matrix operator * (const Matrix&, double);

friend Matrix operator * (const Matrix&, const Matrix&);

friend Vector operator * (const Matrix&, const Vector&);

};

Matrix Translate (const Vector&);

Matrix Scale (const Vector&);

Matrix RotateX (double);

Matrix RotateY (double);

Matrix RotateZ (double);

Matrix Rotate (const Vector& v, double);

Matrix MirrorX ();

Matrix MirrorY ();

Matrix MirrorZ ();

#endif

/****************************************************************************/

#include <math.h>

#include <stdlib.h>

#include "Vector.h"

Vector operator ^ (const Vector& u, const Vector& v)

{

return Vector (u.y * v.z - u.z * v.y, u.z * v.x - u.x * v.z,

u.x * v.y - u.y * v.x);

}

Vector RndVector ()

{

Vector v (rand () - 0.5*RAND_MAX, rand () - 0.5*RAND_MAX, rand () –

0.5*RAND_MAX);

return Normalize (v);

}

Vector& Clip (Vector& v)

{

if (v.x < 0.0)

v.x = 0.0;

else

if (v.x > 1.0)

v.x = 1.0;

if (v.y < 0.0)

v.y = 0.0;

else

if (v.y > 1.0)

v.y = 1.0;

if (v.z < 0.0)

v.z = 0.0;

else

if (v.z > 1.0)

v.z = 1.0;

return v;

}

//////////////////////////////////////////////////////////

// basic vector library //

// all major operators overloaded to support vectors //

//////////////////////////////////////////////////////////

#ifndef __VECTOR__

#define __VECTOR__

#include <math.h>

class Vector

{

public:

double x, y, z;

Vector () {};

Vector (double v) { x = y = z = v; };

Vector (const Vector& v) { x = v.x; y = v.y; z = v.z; };

Vector (double vx, double vy, double vz) { x = vx; y = vy; z = vz; };

Vector& operator = (const Vector& v) { x = v.x; y = v.y; z = v.z;

return *this; };

Vector& operator = (double f) { x = y = z = f; return *this; };

Vector operator - () const;

Vector& operator += (const Vector&);

Vector& operator -= (const Vector&);

Vector& operator *= (const Vector&);

Vector& operator *= (double);

Vector& operator /= (double);

friend Vector operator + (const Vector&, const Vector&);

friend Vector operator - (const Vector&, const Vector&);

friend Vector operator * (const Vector&, const Vector&);

friend Vector operator * (double, const Vector&);

friend Vector operator * (const Vector&, double);

friend Vector operator / (const Vector&, double);

friend Vector operator / (const Vector&, const Vector&);

friend double operator & (const Vector& u, const Vector& v) {

return u.x*v.x + u.y*v.y + u.z*v.z; };

friend Vector operator ^ (const Vector&, const Vector&);

double operator! () { return (double) sqrt (x*x + y*y + z*z); };

double& operator [] (int n) { return * (&x + n); };

int operator < (double v) { return x < v && y < v && z < v; };

int operator > (double v) { return x > v && y > v && z > v; };

};

class Ray

{

public:

Vector Org;

Vector Dir; // direction must be normalyzed

Ray () {};

Ray (Vector& o, Vector& d) { Org = o; Dir = d; };

Vector Point (double t) { return Org + Dir*t; };

};

//////////////////// implementation /////////////////////////

inline Vector Vector:: operator - () const

{

return Vector (-x, -y, -z);

}

inline Vector operator + (const Vector& u, const Vector& v)

{

return Vector (u.x + v.x, u.y + v.y, u.z + v.z);

}

inline Vector operator - (const Vector& u, const Vector& v)

{

return Vector (u.x - v.x, u.y - v.y, u.z - v.z);

}

inline Vector operator * (const Vector& u, const Vector& v)

{

return Vector (u.x * v.x, u.y * v.y, u.z * v.z);

}

inline Vector operator * (const Vector& u, double f)

{

return Vector (u.x * f, u.y * f, u.z * f);

}

inline Vector operator * (double f, const Vector& v)

{

return Vector (f * v.x, f * v.y, f * v.z);

}

inline Vector operator / (const Vector& v, double f)

{

return Vector (v.x / f, v.y / f, v.z / f);

}

inline Vector operator / (const Vector& u, const Vector& v)

{

return Vector (u.x / v.x, u.y / v.y, u.z / v.z);

}

inline Vector& Vector:: operator += (const Vector& v)

{

x += v.x;

y += v.y;

z += v.z;

return *this;

}

inline Vector& Vector:: operator -= (const Vector& v)

{

x -= v.x;

y -= v.y;

z -= v.z;

return *this;

}

inline Vector& Vector:: operator *= (double v)

{

x *= v;

y *= v;

z *= v;

return *this;

}

inline Vector& Vector:: operator *= (const Vector& v)

{

x *= v.x;

y *= v.y;

z *= v.z;

return *this;

}

inline Vector& Vector:: operator /= (double v)

{

x /= v;

y /= v;

z /= v;

return *this;

}

/////////////////////////// Functions /////////////////////////////////

inline Vector Normalize (Vector& v) { return v /!v; };

Vector RndVector ();

Vector& Clip (Vector&);

#endif

Дата добавления: 2014-01-11