Преобразование точек плоскости

Преобразования на плоскости и в пространстве

В соответствии с дискретным принципом работы ЭВМ решение любой задачи разбивается на некоторую последовательность шагов (этапов), образующих алгоритм. В компьютерной графике также выделяются элементарные этапы, из которых составляется графический алгоритм (графические преобразования).

Основу многих операций компьютерной графики составляют так называемые аффинные преобразования. Греческое слово АФФИНИС означает родственный. Аффинная геометрия - раздел геометрии, изучающий свойства фигур на плоскости и в пространстве, сохраняющиеся при любых аффинных преобразованиях, т.е. инвариантных относительно таких преобразований. Аффинные преобразования обеспечивают точечное взаимно однозначное отображение плоскости или пространства на себя, при котором 3 точкам, лежащим на одной прямой, соответствуют 3 точки, также лежащие на одной прямой. Аффинные преобразования переводят пересекающиеся прямые в пересекающиеся прямые, параллельные прямые в параллельные прямые. Плоскость аффинно отображается на некоторую плоскость. Существует множество аффинных преобразований. К ним относятся преобразования подобия, сдвиги, сжатия и др. Следовательно, прорисовываются элементарные операции компьютерной графики, не нарушающие геометрических свойств отображаемого объекта.

Одной из наиболее простых операций преобразования является пересчет координат точки или перенос системы координат. Пусть имеется точка с координатами (x,y). Поставим этим координатам в соответствие координаты (x' = ax + by + c, y' = dx + ey + f), где a,b,c,d,e,f - произвольные числа, связанные неравенством 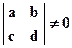. Этот случай можно трактовать двояко:

· сохраняется точка, изменяется система координат (рис. а);

· изменяются координаты точки относительно неизменной системы координат, т.е. формулы задают отображение точки M(x,y) в точку M'(x',y') в той же координатной системе (рис.б).

y y` Рис. а) y Рис. б)

M`

x`

M M

0 x 0 x

Обычно принимается вторая трактовка, т.к. мы работаем в стабильных координатах устройства.

В принципе можно строить изображения в любой системе координат: прямолинейной и криволинейной, прямоугольной и непрямоугольной. Для простоты и в соответствии с привычным представлением будем рассматривать представление в прямоугольной декартовой системе координат.

В машинной графике часто используется матричное представление. Точку можно представить с помощью вектор-столбцов для плоскости 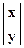, пространства - 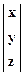. Тогда преобразования точек сводятся к операциям над матрицами, что хорошо соответствует возможностям вычислительной техники. В общем виде задача выглядит так. Даны матрицы A и B и задана их взаимосвязь 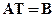. Необходимо найти матрицу преобразования. Решением является 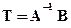, где 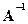- обратная от квадратной матрицы A. Матрица Т - фактически матрица коэффициентов 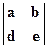. Eё можно трактовать и как оператор. Тогда перемножение матриц используется для того, чтобы выполнить геометрическое преобразование над системой точек, представленных с помощью векторов положения отдельных точек, содержащихся в матрице А. Интерпретация матричного умножения как геометрического оператора является основой математических преобразований в машинной графике.

В аффинных преобразованиях особую роль играют несколько частных случаев, комбинация которых позволяет описать любое преобразование одной точки в другую в соответствии с формулами

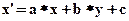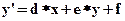; (1)

Фактически эти случаи описывают конкретный вид матрицы Т, т.е. дают коэффициенты преобразования исходных координат точки. Последовательность выполнения этих преобразований - алгоритмы машинной графики.

Начнем рассмотрение элементарных операций с плоскостных. Можно выделить 4 таких операции: поворот, растяжение (сжатие), отражение, перенос.

1. Поворот вокруг начала координат на угол 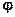описывается формулами ;

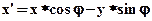y M`

х

Матрица преобразования Т при этом имеет вид: М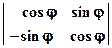

Для частного случая поворота на 90° (поворот против часовой стрелки относительно начала координат) вид матрицы: 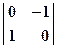. Аналогично выводятся повороты на 180° и 270°, по и против часовой стрелки.

2. Растяжение (сжатие) вдоль координатных осей можно задать в виде:

y .

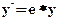M` Матрица Т при этом будет иметь вид 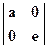. Растяжению мож- но сопоставить положительные, сжатию – отрицательные зна-

M чения коэффициентов. Другое название операции - измене-

0 x ние масштаба. Как частный случай изменения масштаба мо-

жно рассматривать сдвиг вдоль одной из координатных осей. Эти операции перекрываются с ниже рассмотренными операциями зеркального отражения относительно координатных осей.

3. Отражение относительно осей задается матрицами:

Вид матрицы	Действие	Рисунок
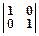
	Положение точки не меняется
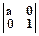
	Изменение положения по оси Х	Y M M` 0 Х
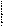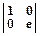
	Изменение положения по оси Y	Y M`   M 0 Х
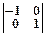
	Зеркальное отражение Относительно оси Y	Y   M M`   0 X
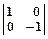
	Зеркальное отражение Относительно оси X	Y M 0 Х M`
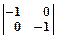
	Зеркальное отражение Относительно начала Координат	Y M 0 Х M`

4. Перенос обеспечивает соотношение 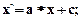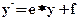у M`

В матричной форме представление будет дано позднее.

В курсе аналитической геометрии доказывается, что любое M

преобразование вида (1) всегда можно представить как суперпозицию 0 x

(последовательное исполнение) простейших 4 преобразований, рассмотренных выше.

Дата добавления: 2014-01-11