Однородные координаты

Применение матрицы общего вида 2*2 к началу координат дает результат:

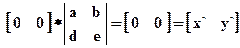
Таким образом, начало координат инвариантно относительно общего преобразования 2х2. Это является ограничением, которое преодолевается с помощью однородных координат.

Пусть М - произвольная точка плоскости с координатами (x,y), вычисленными относительно заданной координатной системы. Однородными координатами этой точки называется любая тройка одновременно неравных нулю чисел x1, x2, x3, связанных с заданными числами соотношением:

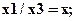
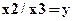
Фактически, однородные координаты дают смещение плоскости, на которой рассматривается фигура, относительно начала координат или, в другой интерпретации, смещение начала координат. Это, по существу, переход в 3-мерному представлению плоских объектов, частный случай пространственного представления.

Рассмотрим более подробно. Введем в 2-мерное представление 3 компонент, равный единице. Тогда вектора будут иметь вид: 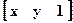; 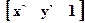. Матрица преобразования примет вид: 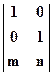, т.к. для выполнения умножения матриц число столбцов, описывающих точку, должно равняться числу строк в матрице преобразования. .

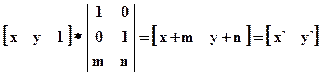Матрица 3*2 не квадратная, поэтому она не имеет обратной матрицы. (Вспомним: даны матрицы 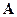и , задана их взаимосвязь 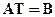. Требуется найти матрицу преобразования. Решением является 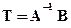, где 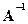- обратная от квадратной матрицы 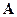. Матрица 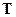- фактически матрица коэффициентов 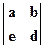, ее можно трактовать и как оператор.) Чтобы получить квадратную обращаемую матрицу преобразования, дополним ее: 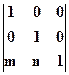. Третья (единичная) компонента векторов точек не меняется при добавлении элементов.

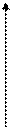z Полученные результаты можно трактовать как поднятие плос-

y кости, в которой мы работаем, на 1 по оси z. В более общем

M`(x,y,1) случае координаты точки можно представить как (hx, hy, h),

h ¹ 0. Следовательно, поднимаем плоскость на h. Практичес-

M(x,y) кий смысл этого связан с изменением масштаба при вписыва-

нии изображения в координаты устройства (мировые координа-

0 х ты - нормированные координаты - координаты устройства).

Как правило, координаты устройства являются целыми числами (пикселы!), следовательно, точку с координатами (0.5, 0.1, 2.5) представить нельзя. При h = 10, получаем (5, 1, 25). Другой случай - координаты (80000 40000 1000), что создает угрозу арифметического переполнения. h = 0,001 дает (80 40 1).

Матрицы третьего порядка позволяют описать любое аффинное преобразование на плоскости. Обычно задачу разбивают на этапы и пользуются 4 элементарными операциями. Матрицы 3 порядка для этих случаев:

1. Вращение (rotation)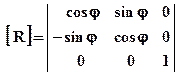

2. Растяжение/сжатие (dilatation)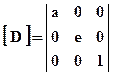

3. Отражение зеркальное (reflection)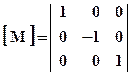

4. Перенос (translation)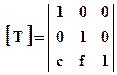

Как использовать эти преобразования? Сначала разбивают действие на элементарные преобразования из 4, приведенных выше, получают матрицы. Потом перемножают эти матрицы в порядке получения. Результирующая матрица является матрицей преобразования.

Дата добавления: 2014-01-11