
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 22
|
|
|
|
Тепловые свойства кристаллов. Тепловое расширение. Теплоемкость кристаллов. Закон Дюлонга и Пти. Трудности классической физики в объяснении температурной зависимости теплоемкости твердых тел.
Тепловое движение частичек в кристаллах существенно отличается от теплового движения молекул в газах и жидкостях. Частички в кристаллах совершают колебания возле положений равновесия – узлов кристаллической решетки. При отклонении частички от положения равновесия возникает сила, которая стремиться вернуть ее в положение равновесия. При малых отклонениях эти силы квазиупругие и колебания частичек гармонические. При комнатных температурах амплитуда колебаний ~ 0,1 межатомного расстояния, это значит 1 – 2 нм.
Тепловые колебания частичек не имеют определенной ориентации. Это сложные колебания, которые определяются связями с соседними частичками. Энергия колебательного движения частичек зависит от температуры и определяет внутреннюю энергию кристалла. При понижении температуры внутренняя энергия уменьшается. Однако при T → 0 внутренняя энергия стремится не к нулю, а, согласно квантовой теории, к некоторому значению U 0, которое называется нулевой энергией. Нулевая энергия обычно значительно меньше энергии взаимодействия частичек.
При нагревании твердые тела расширяются. При увеличении температуры увеличивается амплитуда колебаний и энергия частичек. Однако увеличение амплитуды колебаний не может объяснить тепловое расширение твердых тел, потому что с ростом амплитуды положение равновесия частичек изменяться не должно.
Тепловое расширение вызывается увеличением энергии колеблющихся частичек. Колебания становятся ангармоническим (не гармоническими).
Рассмотрим кривую зависимости потенциальной энергии частичек от расстояния между ними (рис.1):

Рис.1. Тепловое расширение кристаллов: T 4> T 3> T 2> T 1
Пусть горизонтальные прямые показывают уровни энергии атома в кристаллической решетке при разных температурах (T 1, T 2 и т.д.). Точки пересечения прямых с кривой энергии определяют крайние положения атома, которые он занимает при колебаниях. Середина прямой определяет положение равновесия атома при данной температуре.
При повышении температуры атом переходит на более высокие энергетические уровни.
Из-за разной зависимости сил притяжения и отталкивания от расстояния между атомами, кривая потенциальной энергии асимметрична в верхней части.
Вследствие асимметричности кривой зависимости E п(r), центры прямых при повышении температуры смещаются вправо, что означает смещение положения равновесия атома, т.е. увеличение межатомного расстояния.
Следовательно, причиной теплового расширения твердых тел при нагревании является не увеличение амплитуды колебания атомов, а увеличение межатомных расстояний, которые характеризуют новое положение равновесия.
Пусть при температуре T 1 длина тела l, а при температуре T 2 - l′. Опыты показали:
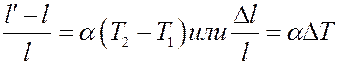 (1)
(1)
где коэффициент пропорциональности α – коэффициент линейного расширения, ∆l / l – относительное удлинение.
Из (1):
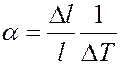 (2)
(2)
Коэффициент линейного расширения численно равен относительному удлинению при повышении температуры на 1K.
Для большинства твердых тел α ≈ 10-5 – 10-6 K-1. Величина α несколько уменьшается с понижением температуры.
Из-за анизотропии кристаллов, коэффициент линейного расширения разный для разных направлений. Поэтому, если в кристалле провести произвольную прямую, то при повышении температуры она не будет оставаться прямой.
Однако в любом кристалле существуют такие направления, вдоль которых прямая будет оставаться прямой и при тепловом расширении кристалла. Такие направления называются кристаллографическими осями.
Значения коэффициента линейного расширения вдоль этих осей называются главными. В зависимости от типа решетки, кристаллы могут иметь одну (одноосные), две (двухосные), три (трехосные) кристаллографические оси и, соответственно, один, два, три главных коэффициента линейного расширения.
При нагревании возрастает, и объем твердого тела. Установлено, что относительное изменение объема тела пропорционально изменению температуры:
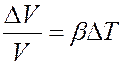 (3)
(3)
где ∆V / V – относительное изменение объема тела при изменении температуры на ∆T. Коэффициент пропорциональности β называется коэффициентом объемного расширения:
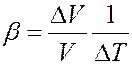 (4)
(4)
Коэффициент объемного расширения численно равен относительному изменению объема при изменении температуры на 1K.
Если α 1, α 2, α 3 – главные коэффициенты линейного расширения кристалла, то коэффициент его объемного расширения определяется выражением:
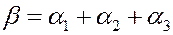 (5)
(5)
Для кристаллов с кубической решеткой и для всех изотропных тел:
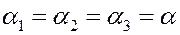 (6)
(6)
Для этих тел:
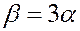 (7)
(7)
Если при нагревании твердое тело не имеет возможности свободно расширяться, то возникают очень большие напряжения, которые надо учитывать на практике.
При нагревании твердого тела теплота идет на увеличение энергии колебаний атомов. Энергия колебательного движения складывается из кинетической и потенциальной энергии. Каждое колебание можно разложить на три составляющих по осям координат. Поэтому каждая частица обладает тремя колебательными степенями свободы iк = 3.
При гармонических колебаниях кинетическая энергия колебательного движения равна потенциальной. Согласно закону равномерного распределения энергии по степеням свободы на каждую колебательную степень свободы приходится 1/2 kT в виде кинетической энергии и 1/2 kT в виде потенциальной. Следовательно, полная энергия колеблющейся частицы будет равна:
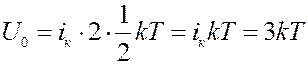 (8)
(8)
Внутренняя энергия 1 моля твердого тела:
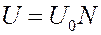 (9)
(9)
где N – число частиц в одном моле твердого тела.
Для химически простых веществ число частиц в 1 моле равно числу Авогадро N = Na. Тогда из (8) и (9):
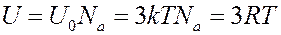 (10)
(10)
Коэффициент объемного расширения твердых тел очень мал, поэтому Cp ≈ CV = C. Следовательно, вся теплота, подведенная к твердому телу, идет на увеличение его внутренней энергии. Тогда молярная теплоемкость твердого тела:
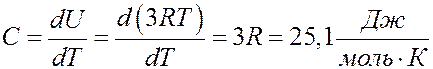 (11)
(11)
Согласно (11) молярная теплоемкость химически простых твердых тел равна 3 R и не зависит от температуры. Это закон Дюлонга и Пти (1818г.). Закон Дюлонга и Пти хорошо выполняется для многих веществ при комнатных температурах.
При определении молярной теплоемкости химически сложных веществ необходимо учитывать общее число частиц в 1 моле данного вещества. У химически сложных веществ общее число частиц в 1 моле равно числу Авогадро умноженному на число атомов, из которых складывается молекула данного вещества. Например, KCl – в одном моле Na атомов калия и Na атомов хлора – всего 2 Na частиц. Молярная теплоемкость такого кристалла 2*3 R = 6 R. В случае трехатомных молекул молярная теплоемкость 9 R, четырехатомных - 12 R.
Эти рассуждения совпадают с эмпирически установленным законом Неймана-Коппа:
Молярная теплоемкость твердых соединений равна сумме атомных теплоемкостей элементов, которые входят в это соединение:
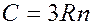 (12)
(12)
где n – число атомов, входящих в молекулу данного соединения.
Этот закон, также как и закон Дюлонга и Пти выполняется при довольно высоких температурах, при которых колебания частиц можно считать независимыми.
Некоторые вещества не подчиняются закону Дюлонга и Пти. Молярная теплоемкость алмаза при комнатных температурах, много меньше 3 R, и только при температурах больших, чем 1000 оC она приближается к значению 3 R.
Это не единственное отклонение от закона Дюлонга и Пти. При низких температурах теплоемкость кристаллических веществ быстро уменьшается и стремится к нулю при абсолютном нуле температуры (рис.2).
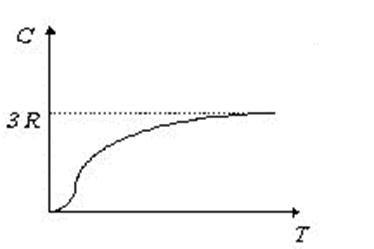
Рис.2. Зависимость теплоемкости от температуры
Вблизи абсолютного нуля теплоемкость всех кристаллов пропорциональна T 3, и только при достаточно высокой температуре, характерной для каждого вещества, начинают выполняться законы Дюлонга и Пти (11) и Неймана-Коппа (12).
Эти законы являются следствием закона о равномерном распределении энергии по степеням свободы. Тот факт, что твердые тела не подчиняются этим законам, свидетельствует о том, что закон о равномерном распределении энергии по степеням свободы является приблизительным, и не применим при низких температурах.
Точная, квантовая теория теплоемкости кристаллов была создана Эйнштейном и Дебаем. Квантовая теория теплоемкости учитывает:
1. Квантование энергии колебательного движения – энергия колебательного движения может принимать только некоторые, дискретные значения;
2. Колебания частиц в кристаллической решетке не являются независимыми.
Из теории Дебая следует, что при температурах близких к абсолютному нулю, внутренняя энергия твердого тела пропорциональна четвертой степени температуры:
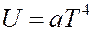 (13)
(13)
где a – постоянная, зависящая от частоты колебаний частиц.
Следовательно, теплоемкость кристаллов:
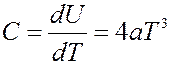 (14)
(14)
(14) – закон кубов Дебая. Из теории Дебая следует, что, начиная с некоторой температуры разной для разных веществ (характеристическая температура Дебая) теплоемкость начинает быстро уменьшаться с понижением температуры.
Температура Дебая считается границей между низкими и высокими температурами (и не только для теплоемкости). Температура Дебая для серебра – 210 oC, алюминия – 400 oC, алмаза – 2000 oC.
Для кристаллов, не подчиняющихся закону Дюлонга и Пти при комнатных температурах (алмаз, бор, кремний), характеристические температуры больше 1000 oC, и поэтому комнатные температуры являются для них низкими.
Как показали опыты, для некоторых веществ теплоемкость пропорциональна T 2, а для некоторых ~ T. Это связано с особенностями строения кристаллической решетки. Если частицы связаны с соседними частицами одинаково сильно во всех трех направлениях – выполняется закон кубов Дебая. Если вещество имеет слоистую структуру (графит, слюда), то связь частиц в двух направлениях (в одной плоскости) сильнее, чем в третьем направлении (между слоями). Для этих веществ теплоемкость ~ T 2. Если вещество складывается из частиц с цепочной связью и цепи связаны между собой слабо, то теплоемкость ~ T (HF, BiO3, плавленый кварц).
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2162; Нарушение авторских прав?; Мы поможем в написании вашей работы!