
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение со сверхзвуковой скоростью. Скачки уплотнения. Ударные волны. Число Маха. Реактивные двигатели. Многоступенчатые ракеты
|
|
|
|
Лекция 25
Как было показано выше скорость газового потока, вытекающего из отверстия, не может быть выше критической скорости, равной скорости распространения звука в газе при температуре равной критической:
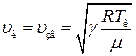
где u 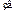 – скорость звука в газе.
– скорость звука в газе.
Однако, изменяя профили трубопровода можно регулировать режим истечения газа. При этом можно использовать избыточное давление, возникающее в потоке при критическом истечении и получить скорости истечения газа большие, чем звуковые (так называемые сверхзвуковые скорости). С физической точки зрения эта задача заключается в том, чтобы определить условия, при которых беспорядочное тепловое движение молекул в газовом потоке, который движется со скоростью звука, частично превратить в упорядоченное движение и, таким образом, получить сверхзвуковые скорости истечения газового потока.
Определим эти условия. Расход газа через любое сечение выходного отверстия величина постоянная:
ruS = const (1)
Уравнение (1) это уравнение неразрывности потока сжимаемого газа. Продифференцируем (1):
rudS + r Sdu + uSdr = 0
Разделим полученное уравнение на ruS:
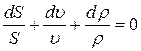
или:
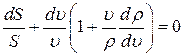 (2)
(2)
Однако:
 (3)
(3)
Из предыдущего параграфа известно, что:
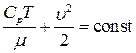
Продифференцируем это уравнение:

Отсюда:
 (4)
(4)
Определим второе слагаемое в скобках в уравнении (2). Для этого подставим (3) и (4) в это слагаемое:
 (5)
(5)
Запишем уравнение Пуассона в переменных T и V и продифференцируем его:
TVg -1 = const
Vg -1 dT + T (g -1) V g -2 dV = 0
Умножив последнее уравнение на V - g+ 2 получим:
VdT + T (g -1) dV = 0
или:
 (6)
(6)
Подставим (6) и (5):
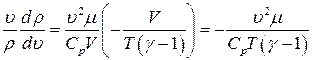
Учитывая, что:
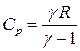 ,
,
получаем:
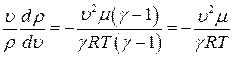 (7)
(7)
В (7)
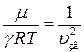
где u зв – скорость звука в газе. С учетом этого перепишем (7) в виде:
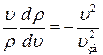 (8)
(8)
Подставим (8) в (2):
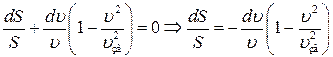
или:
 (9)
(9)
Из уравнения (9) следует, что при u < u 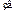 , du / dS < 0. Это значит, что если газ вытекает через трубу переменного сечения со скоростью меньшей чем критическая (скорость звука), то du / dS < 0 и его скорость увеличивается в той части, где труба сужается (dS < 0 Þ du > 0) и уменьшается там, где труба расширяется (dS > 0 Þ du < 0). И наоборот при истечении газа со скоростями большими чем критическая (u > u
, du / dS < 0. Это значит, что если газ вытекает через трубу переменного сечения со скоростью меньшей чем критическая (скорость звука), то du / dS < 0 и его скорость увеличивается в той части, где труба сужается (dS < 0 Þ du > 0) и уменьшается там, где труба расширяется (dS > 0 Þ du < 0). И наоборот при истечении газа со скоростями большими чем критическая (u > u 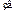 ) du / dS > 0. Это значит, что при истечении через расширяющиеся участки трубы скорость истечения возрастает (dS > 0 Þ du > 0) и становится больше критической. В этом случае увеличение кинетической энергии потока происходит за счет уменьшения внутренней энергии газа.
) du / dS > 0. Это значит, что при истечении через расширяющиеся участки трубы скорость истечения возрастает (dS > 0 Þ du > 0) и становится больше критической. В этом случае увеличение кинетической энергии потока происходит за счет уменьшения внутренней энергии газа.
Для получения сверхзвуковых скоростей истечения газового потока Лавалем, Стэнтоном, Франклем были разработаны сверхзвуковые сопла (каналы, трубы переменного сечения), в которых происходит ускорение газового потока до скоростей больших, чем скорость звука (рис.1).

Рис.1. Сечения различных сопел
В сопле Лаваля в сужающейся части скорость газового потока увеличивается от 0 до звуковой скорости (докритичное течение газа), затем газовый поток попадает в расширяющуюся часть сопла, где скорость его истечения увеличивается до сверхзвуковой скорости.
Расширяющиеся сопла используются в паровых и газовых турбинах, реактивных двигателях и других устройствах.
Превышение скорости звука в газовых средах приводит к ряду явлений, которые надо учитывать при движении самолетов, снарядов, ракет, лопаток газовых турбин и т.д.
Когда какое-нибудь тело (источник возмущения) движется в газовой среде со скоростью меньшей, чем скорость звука, то возмущения среды (упругие деформации), которые возникают из-за взаимодействия среды с передней поверхностью тела распространяются во все стороны со скоростью звука и обгоняют его. Если источник движется со сверхзвуковой скоростью, то упругие деформации среды, вызванные им не обгоняют источник возмущения, они отстают от него и остаются внутри так называемого конуса возмущений или конуса Маха (рис.2).
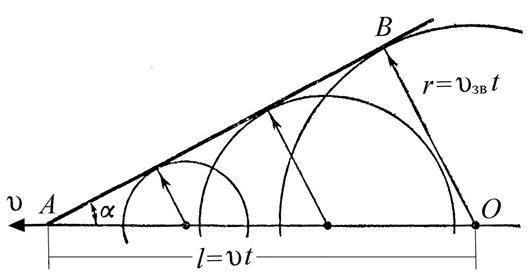
Рис. 2. К определению числа Маха
Если источник возмущения за время t переместится из точки O в точку A, то OA = l = u t. Возмущение движется со скоростью звука и за это время проходит расстояние OB = r = u 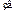 t.
t.
Из рисунка видно, что:
 (10)
(10)
Отношение скорости движения тела в среде к скорости звука в этой среде называется числом Маха:
 (11)
(11)
Если M > 1, то u > u 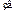 , наблюдается движение со сверхзвуковой скоростью. При движении со сверхзвуковыми скоростями возникают скачки уплотнения (скачки давления) – тонкие слои среды с толщиной порядка средней длины свободного пробега молекул, в которых скачкообразно изменяются термодинамические параметры газа (давление, плотность и т.д.). Скачки уплотнения создают в пространстве ударные волны. Ударные волны представляют собой поверхность разрыва непрерывности физических свойств среды. Ударные волны возникают также при различных взрывах (бомбы, снаряды и т.д.), при прохождении через газ электрических разрядов (молнии).
, наблюдается движение со сверхзвуковой скоростью. При движении со сверхзвуковыми скоростями возникают скачки уплотнения (скачки давления) – тонкие слои среды с толщиной порядка средней длины свободного пробега молекул, в которых скачкообразно изменяются термодинамические параметры газа (давление, плотность и т.д.). Скачки уплотнения создают в пространстве ударные волны. Ударные волны представляют собой поверхность разрыва непрерывности физических свойств среды. Ударные волны возникают также при различных взрывах (бомбы, снаряды и т.д.), при прохождении через газ электрических разрядов (молнии).
Скачкообразные изменения плотности могут быть настолько значительными, что области их проявления можно фотографировать. Скачки уплотнения в зависимости от их геометрической формы делятся на косые и прямые (рис.3).

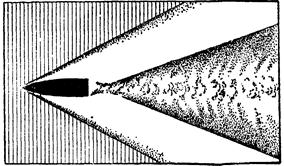
Рис.3. Прямой и косой скачки уплотнения
Возникновение скачков уплотнения вызывает сопротивление движению тел, которое в отличие от малых скоростей (F ~ u) пропорционально квадрату скорости (F ~ u 2).
Для уменьшения сопротивления крыльев летательных аппаратов при не очень больших M используют стеловидные и треугольные формы (крылья, пули, снаряда, ракеты и т.д.), передняя кромка которых образует острые углы с направлением скорости набегающего потока.
При больших M кинетическая энергия потока много больше энтальпии, поэтому изменением энтальпии можно пренебречь. В этих случаях течение потока перестает зависеть от M, а значит и от формы тела. Поэтому форму передней части ракет делают тупой, потому что стабилизация течения около тупых тел наступает при меньших значениях M, чем около заостренных.
При ускоренном истечении газа из сопла газовый поток порождает реактивную силу, приложенную к соплу и направленную в противоположную сторону направлению ускорения газового потока. Эта сила равна приращению (изменению) импульса газового потока в единицу времени.
Реакция газового потока используется в реактивных двигателях. Основным элементом любого реактивного двигателя является сопло (Лаваля, Франкля, и т.д.), которое необходимо для получения максимально возможной скорости вытекания газового потока. Реактивные двигатели делятся на две группы: воздушно-реактивные двигатели (ВРД) и ракеты.
Прямоточный ВРД работает и создает реактивную тягу в том случае, когда он движется с большой скоростью (рис.4).

Рис. 4. Схема прямоточного воздушно-реактивного двигателя
Для воздушно-реактивного двигателя необходимо только топливо (керосин). Окислителем и одновременно рабочим телом, которое и создает тягу, является атмосферный воздух. В ракетных двигателях используется и топливо, и специальные окислители, поэтому работа таких двигателей не зависит от состояния окружающей среды. Они могут работать и в вакууме.
Рассмотрим схему прямоточного воздушно-реактивного двигателя (рис.4).
В области за входным соплом скорость газового потока (дозвуковая) уменьшается, потому что площадь поперечного сечения возрастает (ruS = const). Газовый поток тормозится в расширяющемся канале, при этом скорость уменьшается, а давление плотность и температура возрастают. В камере сгорания впрыскивается топливо. При сгорании топлива возрастает внутренняя энергия газа. Из камеры сгорания газ попадает в выходное сопло Лаваля. В месте наибольшего сужения сопла скорость газового потока равна скорости звука. После расширения газа в широкой части сопла его скорость увеличивается и из сопла вытекает сверхзвуковой газовый поток. Эти двигатели очень просты и надежны. Они пригодны для наиболее скоростных самолетов (M ≥ 4).
Турбокомпрессорный ВРД. Турбокомпрессорные двигатели могут работать при любых скоростях. В отличие от прямоточных ВРД сжатие воздуха в камере сгорания осуществляется компрессором (рис.5).
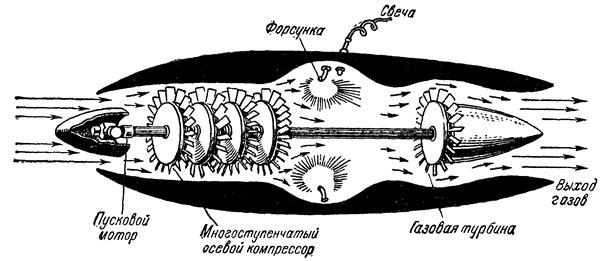
Рис. 5. Схема турбореактивного двигателя
Энергия газового потока продуктов сгорания топлива за камерой сгорания частично передается турбине, которая приводит в действие компрессор, сжимающий газ перед камерой сгорания. Турбина и компрессор закреплены на одной оси. В некоторых модификациях двигателей турбина приводит во вращение лопасти пропеллера (турбовинтовые двигатели). Оставшаяся часть энергии газового потока создает реактивную тягу в выходном сопле.
Ракетные двигатели делятся на твердотопливные (пороховые) ракетные двигатели (ТРД) и жидкостные ракетные двигатели (ЖРД). В этих двигателях ускорение потока газа осуществляется за счет химической (в будущем за счет ядерной, световой) энергии. Ракетный двигатель единственный двигатель, который может работать в безвоздушном пространстве, и пригоден для космических перелетов.
Пороховые ракеты состоят из камеры сгорания с пороховым составом, выходного сопла и зажигательного устройства. ЖРД состоят из камеры сгорания с форсунками для подачи топлива и окислителя, устройства зажигания, сопла, турбонасосов и баков с топливом и окислителем (рис.6).

Рис. 6. Схема жидкостного ракетного двигателя
ЖРД конструктивно более сложен, чем ТРД, однако в них можно регулировать процесс сгорания топлива, и, таким образом, силу тяги ракеты.
В зависимости от требуемой конечной скорости ракеты могут быть одноступенчатые и многоступенчатые. Каждая ступень ракеты (кроме полезного груза) представляет собой автономный блок с собственным двигателем, топливом и окислителем. После сгорания всего топлива, соответствующая ступень ракеты отделяется от остальной части ракеты, вследствие чего масса оставшейся части ракеты уменьшается, а скорость, которую сообщает ей двигатель следующей ступени, увеличивается.
Космический ракета “Восток” – 12.04.1961г. Космонавт Ю.А. Гагарин. Трехступенчатая жидкостная ракета, длина – 38 метров, диаметр 10 метров.
Литература:
1. М.С.Цэдрык. Курс агульнай фізікі. Мн., 1994г.
2. А.К.Кинкоин, М.К.Кикоин. Молекулярная физика. М.,.1976.
3. Р.В.Телесин. Общий курс физики. т. П, М.,
4. С.Д. Шебалин. Молекулярная физика. М.,
5. Н.В.Савельев. Курс обшей физики. т.І, М.,
6. Н.Ф.Яковлев. Курс физики. Теплота и молекулярная физика. М., 1976.
ОГЛАВЛЕНИЕ
Предисловие.. 2
Основы молекулярно-кинетической теории (МКТ). 3
Лекция 1 Предмет молекулярной физики. Основные положения молекулярно-кинетической теории (МКТ) вещества и их экспериментальное обоснование. Статистический и термодинамический подходы к изучению макроскопических систем. Флуктуации и их проявления. 3
Лекция 2 Давление газа. Абсолютная температура. Молекулярно-кинетическое обоснование абсолютной температуры и давления. Измерение давления и температуры. 10
Лекция 3 Идеальный газ. Основное уравнение молекулярно – кинетической теории газов. Постоянная Больцмана. Температура и давление как статистические величины. 16
Лекция 4 Уравнение состояния идеального газа. Универсальная газовая постоянная. Основные газовые законы. 22
Лекция 5 Распределение скоростей молекул по Максвеллу. Измерение скоростей молекул. Опыт Штерна. Опытная проверка распределения молекул по скоростям. 30
Лекция 6 Газ в силовом поле. Барометрическая формула. Распределение Максвелла – Больцмана. Экспериментальное определение числа Авогадро. 39
Явления переноса в газах.. 45
Лекция 7 Средняя длина и среднее время свободного пробега молекул. Явления переноса в газах. Диффузия. 45
Лекция 8 Внутреннее трение (вязкость газов). Теплопроводность газов. 52
Лекция 9 Теплопроводность и внутреннее трение при низких давлениях. Технический вакуум. Получение и методы измерения низких давлений. 58
Основы термодинамики.. 68
Лекция 10 Термодинамическая система (ТДС). Параметры состояния. Термодинамическое равновесие. Внутренняя энергия. Взаимодействие ТДС. Работа и теплота как форма обмена энергиями между ТДС. Равновесные и неравновесные процессы. Функции состояния и функции процесса. 68
Лекция 11 Первое начало термодинамики. Применение I начала термодинамики к изопроцессам. Адиабатный процесс. Уравнение Пуассона. Скорость звука в газах. 74
Лекция 12 Политропический процесс. Теплоемкость. Принцип равномерного распределения энергии по степеням свободы и границы его применимости. 86
Лекция 13 Второе начало термодинамики. Невозможность создания вечных двигателей. Обратимые и необратимые процессы. Круговые процессы. Тепловые машины. Цикл Карно. 95
Лекция 14 Теоремы Карно. Реальные циклы. Приведенная теплота. Энтропия. Закон возрастания энтропии в изолированной системе. 102
Лекция 15 Статистический характер II начала термодинамики. Теорема Нернста. Недостижимость абсолютного нуля температуры. 113
Реальные газы и жидкости.. 119
Лекция 16 Отступление реальных газов от законов для идеальных газов. Взаимодействие молекул. Уравнение Ван-дер-Ваальса и его анализ. Критическое состояние. Экспериментальные изотермы реального газа. Сопоставление изотерм Ван-дер-Ваальса с экспериментальными изотермами. 119
Лекция 17 Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Сжижение газов. Получение низких температур. 128
Лекция 18 Фазовые переходы I рода. Равновесие жидкости и пара. Свойства насыщенного пара. Уравнение Клапейрона-Клаузиуса. Понятие о фазовых переходах II рода. Влажность воздуха. Особенности фазовых переходов воды и их роль в природе. 140
Лекция 19 Свойства жидкого состояния. Поверхностный слой. Поверхностное натяжение. Смачивание. Формула Лапласа. Капиллярные явления. 142
Лекция 20 Давление насыщенного пара над мениском. Растворы. Осмос. Осмотическое давление. Закон Вант-Гоффа. 142
Твердые тела.. 142
Лекция 21 Аморфные и кристаллические тела. Анизотропия кристаллов. Классификация кристаллов по типу связей. Дефекты в кристаллах. Жидкие кристаллы. 142
Лекция 22 Тепловые свойства кристаллов. Тепловое расширение. Теплоемкость кристаллов. Закон Дюлонга и Пти. Трудности классической физики в объяснении температурной зависимости теплоемкости твердых тел. 142
Лекция 23 Плавление и кристаллизация. Диаграмма равновесия твердой, жидкой и газообразной фаз. Тройная точка. 142
Газодинамика.. 142
Лекция 24 Основное уравнение газодинамики. Адиабатное течение газов. Критическая скорость. 142
Лекция 25 Движение со сверхзвуковой скоростью. Скачки уплотнения. Ударные волны. Число Маха. Реактивные двигатели. Многоступенчатые ракеты. 142
Литература: 142
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 3130; Нарушение авторских прав?; Мы поможем в написании вашей работы!