Garmonic balance method. Two aspects of nonlinearity: soft and rigid. A resonance in the nonlinear oscillator

Acquaintance with a garmonic balance method, with features of a resonance in the nonlinear high-frequency injection unit as developing process of the basic fundamental phenomenon in nonlinear systems, - is the purpose of the given lecture.

It is a method of the analytical description of stationary waves in poorly nonlinear systems. It is a crude method. Approach consists that we consider forced oscillations in poorly nonlinear system, called by a harmonious superposed force, is strict harmonic oscillations and we write down them in an aspect:

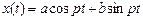. (1)

Higher harmonics 2р, 3р … np we neglect, and the information on nonlinearity of system we keep in required amplitudes an and b harmonic oscillations. This assumption physically well justifies in systems poorly nonlinear with a weak dissipation. Really, at small attenuation in LC - system the resonance is expressed strongly. Hence, higher harmonics 2р, 3р … forced oscillations will be suppressed"in comparison with a first harmonic.

Let's down the equation for oscillations in poorly nonlinear conservative system:

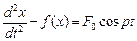. (2)

Let's substitute in it expression (1). Function 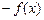we expand into a series the Fourier:

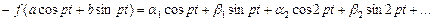(3)

Let's note that a term of equation α₀, expressing a constant componenet, there is messed, as nonlinearity contains only in reactive elements. All coefficients it is found under known formulas:

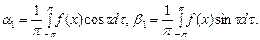(4 )

At substitution in the 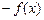equation (3) we will be restricted only to its harmonious approach, i.e. we kick all members containing higher harmonics of a superposed force. As a result we gain the equation

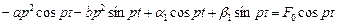. (5)

Collecting separately all members with sine and косинусами, we gain two algebraic equations for the description of resonance curves:

. (6)

In the beginning we observe a case (oscillations in system can be only at the expense of an initial stock of energy in it). For this case the solution of the equations gives us values of frequencies free nonisochronous:

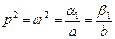. (7)

Then we solve the equation:.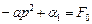

Дата добавления: 2014-01-11