
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Self-excited vibrations. The basic definitions and concepts
|
|
|
|
L
ω C (t)
Emcospt
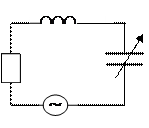
Fig. 1. Instances of oscillations for mechanical () and electric () systems.
The differential equation for charge oscillations on the capacitor in a contour represented on fig. 1 looks like:
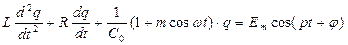 . Thus, on studied oscillatory system two energy sources act: a signal source (w) and the pump source (). At a weak resonance parametre modulation () for the account of act of the pump source increases attenuations in system. It means that the part of the energy gained by system from a source of a signal, is transferred by it to the pump source.
. Thus, on studied oscillatory system two energy sources act: a signal source (w) and the pump source (). At a weak resonance parametre modulation () for the account of act of the pump source increases attenuations in system. It means that the part of the energy gained by system from a source of a signal, is transferred by it to the pump source.
In case of a strong resonance modulation of magnitude of parametre has the consequence the contribution of energy from the pump source in oscillatory system. In the case under consideration this contribution occurs in signal oscillations, i.e. the signal gains in strength in comparison with a signal at a usual resonance, in a linear oscillating circuit with other things being equal. At increment m, the denominator in expression for amplitude is aimed to null i.e. 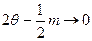 , it testifies to loss by system of stability and about origination possibility in it of parametric vibrations.
, it testifies to loss by system of stability and about origination possibility in it of parametric vibrations.
Lecture 11
Parametric excitation and amplification of electric oscillations.
The lecture purpose is acquaintance with parametric amplification and generation principles and features of parametric amplifiers.
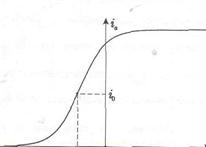
Method of excitation and reinforcement of electromagnetic modes in which power amplification occurs for the account of the energy spent for periodic change of magnitude of jet parametre (inductance L or capacity ) oscillatory system. We observe a principle of a parametric amplification and generation on an instance of the elementary system — the oscillating circuit consisting of fixed resistance R, inductance L and capacity C which periodically changes in a time (fig. 1). At a resonance (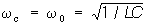 where wс — frequency of a reinforced signal, w0 — natural frequency of a contour) the charge q on condenser coatings changes in a manner: q = q 0sinwc t. =. The electrostatic energy W reserved in the capacitor, is equal:
where wс — frequency of a reinforced signal, w0 — natural frequency of a contour) the charge q on condenser coatings changes in a manner: q = q 0sinwc t. =. The electrostatic energy W reserved in the capacitor, is equal:
W = (q 2/2 C) = (q 20/4 C) (1-cos 2wc t). Whence it is visible that W changes with frequency, the equal doubled signal frequency. If during the moment when q = q 0, capacity of the capacitor With jump to change on D С (for example, to telescope capacitor plate) the charge q has not time to change, and energy W changes on

Magnitude (if s/with <<1): D W =- W D C/C. A Fig. 1
From this it follows that результирующее energy increase in a contour at periodic change With maximum if to reduce capacity during the moments when q it is maximum, and to refund magnitude of capacity to a reference value at q = 0. It means that if to change With with frequency wн = 2wс and with a certain phase (fig. 1) the device changing With, as though «pumps energy» in a contour twice for period of oscillations.
|
|
|
Lecture 12
Acquaintance with one of remarkable and not trivial developing processes of nonlinearity – self-excited vibrations - is the lecture purpose.
Along with oscillatory systems in which energy can decrease eventually only because of a dissipation, exist also such in which vibrational energy replenishment for the account неустойчивостей is is possible. It can occur, when the system in a condition to exchange energy or substance with a circumambient, i.e. is energetically not isolated (opened). In open systems there is an assemblage of basic new phenomena, first of all — generation of self-excited vibrations. "The self-excited vibration" term injected A.A.Andronov in 1928 It laid the foundation for the theory of self-excited vibrations, for the first time connecting them with Poincare's limiting cycles.
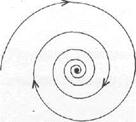
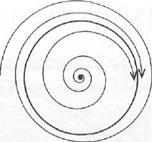
Modern definition of self-excited vibrations can be formulated as follows. Self-excited vibrations are continuous oscillations in nonlinear диссипативной to system, an aspect and which properties are defined by the system and do not depend on entry conditions (at least, in final limits). In this definition the demand of independence of entry conditions is key. Eventually the phase path is aimed to some attracting assemblage named аттрактором. After transient in system oscillations to which traffic of a representing point on аттрактору answers are installed. Such oscillations, obviously, will depend only on system parametres, instead of from entry conditions. Words «at least, in final limits» mean that, basically, can exist a little аттракторов, each of which has the basin of an attraction, i.e. area in a phase space, whence phase paths are aimed to given аттрактору.,
Аттракторами, to periodic self-excited vibrations, resistant to limiting cycles are matching. Discriminate also quasiperiodic, i.e. containing a little independent spectral a component, being in an irrational relationship, and also chaotic self-excited vibrations which are casual though are made under the influence of not casual energy sources. A spectrum of chaotic self-excited vibrations the continuous. Mathematical image of quasiperiodic self-excited vibrations in a phase space is the n-dimensional torus, and stochastic — strange аттрактор, i.e. the attracting assemblage having extremely difficult internal structure on which all (or nearly so all) paths are unstablis. Here we concentrate in the core on studying of periodic self-excited vibrations.
Lecture 13
The generalised circuit design of the radio engineering oscillator the Van-der-Pol Equation
The lecture purpose is studying of the oscillator of self-excited vibrations, reception of the equation of the Van-der-field – the basic model for the analysis of periodic self-excited vibrations, definition of conditions of excitation and a finding of stationary conditions.
(Fig. 1) serves as oscillatory system of the oscillator RLC - a contour. Voltage from a contour moves on an entry of an active element — the amplifier. We will consider that the nonlinear characteristic of the amplifier, i.e. dependence of a current on an amplifier exit i from voltage on an entry and which can be approximated a cubic polynomial is known
|
|
|
i (u) = g0u-g2u3 +.... Factors gn are considered as the positive. We yet do not concretise the physical nature of the amplifier. The amplifier exit is loaded on the coil of inductance L1 which is inductive is connected with the contour coil. Thus the return coupling is provided.
|
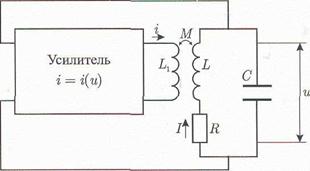
Fig. 1. The circuit design of the radio engineering oscillator of self-excited vibrations.
The mechanism of excitation of self-excited vibrations in the oscillator can be presented qualitativly as follows. Even in the absence of voltage on an exit of the amplifier voltage in a contour tests random fluctuations. They gain in strength the amplifier and again arrive in a contour through a return coupling chain. Thus from a noise spectrum of fluctuations the component on natural frequency высокодобротного a contour will deposit. If the energy which is brought in to a contour, thus, surpasses energy of losses, the amplitude of oscillation builds up. For this purpose it is necessary, that the coefficient of amplification was great enough. However, as dependence i (u) is nonlinear, with growth u the coefficient of amplification drops that leads to determination of stationary self-excited vibrations with constant amplitude in what the mechanism of nonlinear restriction of unstable stability consists. Thus, nonlinearity in hunting systems plays a basic role, controlling receipt of energy from a source. In linear system (for example, the high-frequency injection unit with a negative friction) the amplitude of oscillation would build up indefinitely.
Lecture 14
The Van-der-Pol and Relej equations. Andronov's branching — Hopfa
The lecture purpose is studying of dynamics of amplitude of self-excited vibrations at change бифуркационного parametre and conversion of phase portraits at supercritical Andronov's branching — Hopfa.
As the basic models for the analysis of periodic self-excited vibrations the Van-der-field and 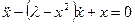 Relej equations serve
Relej equations serve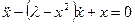
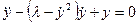 .
.
As it has been shown earlier, autoexcitation of self-excited vibrations occurs at λ> 0. In process of magnification λ there is a step-by-step passage from weakly nonlinear quasi-harmonic oscillations to the relaxational. In the given lecture we consider these modes in more details.
Used an averaging method it is possible to receive expression of dependence of a square of amplitude of oscillations from time
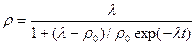
| 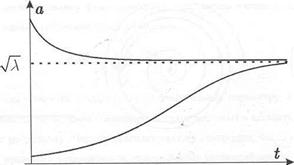 Fig. 1 Fig. 1
|
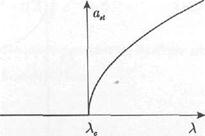
Thus, when bifurcation parameter λ, transits critical value λρ =0, the phase portrait of system is transformed as follows. If λ <λρ on a phase plane there is a unique equilibrium state of type steady focus. If λ> λρ it becomes unstable and in its neighborhood there is a steady limiting cycle. The characteristic size of a limiting cycle (i.e. amplitude of stationary self-excited oscillations) increases proportionally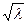 . Such bifurcation is called as Andronov- Hopf's normal (supercritical) bifurcation.
. Such bifurcation is called as Andronov- Hopf's normal (supercritical) bifurcation.
|
|
|
The term "supercritical" is connected by that the limiting cycle originates only after the parametre exceeds critical value. As the amplitude of oscillation with growth X smoothly increases from null, say that autoexcitation occurs softly.
Lecture 15
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 646; Нарушение авторских прав?; Мы поможем в написании вашей работы!