Auto-oscillation system with a hard mode

The lecture purpose – acquaintance with features of a subcritical branching of Andronov-Hopf on an instance of a hunting system with a hard excitation.

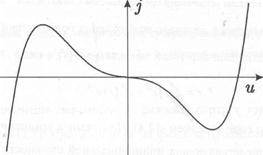
Let's observe the oscillator on an active element with the negative differential conductivity ­which ­ voltage-current characteristic it is possible to approximate as follows ­(fig. 1а):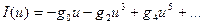

Inducting new variables, instead of the Van-der-field equation we gain, where λ and μ – dimensionless parameters.

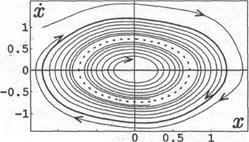
The condition of stability of a fixed point still looks like λ <0 (e.e. g₀ <G). However, even if it is done, self-excited oscillations nevertheless can arise, if initial perturbation is great enough. Really, from the equation (1) it is visible that the member proportional μх², represents some kind of the negative nonlinear –attenuation (if μ> 0). When the amplitude of initial perturbation exceeds some critical value, non-linear gain exceeds­ the linear attenuation and oscillations start to rise. In that case speak about hard mode excitation. On a phase plane there are two attractors: a type equilibrium state ­steady focus and a steady limiting cycle. Each attractor has the pool­ of an attraction which are differentiated by an unstable limiting cycle.

Known to everyone example of self-oscillatory system with hard mode excitation are a pendulum ­ wag-on-the-wall. Really, after clock are got, i.e. the weight is lifted on necessary height, it is necessary to inform a pendulum an initial push that he started to fluctuate.

Literature

1. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний, М.: Наука, 1992.

2. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Радио и связь”, 1981.

3. Горелик Г.С. Колебания и волны. М.: Сов.радио, 1959.

4. Теория колебаний./ Под. ред. К.Я. Сенаторова. М.: Изд. МГУ, 1983.

6. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Радио и связь, 1981.

7. Горелик Г.С. Колебания и волны. М.: Сов.радио, 1959.

8. Кроуфорд Ф. Берклиевский курс физики. т.III. Волны. М.: Наука, 1976.

9. Рыскин Н.М., Трубецков Д.И. Нелинейные волны, М.: Наука, 2000.

10. Ланда П.С. Нелинейные колебания и волны, М.: Наука, 1997.

11. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. М.: Наука, 1987

13. Пиппард А. Физика колебаний./ Пер. с англ. Под ред. А.Н.Матвеева, М.: Высш. шк., 1985.

14. Заславский Г.М., Сагдиев Р.З. Введение в нелинейную физику: от маятника до турбулентности и хаоса.. М.: Наука, 1988.

15.Сборник задач по теории колебаний./ Под. ред. Постникова Л.И. и Королева В.И.,. М.: Наука, 1978.

16. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент: Введение в нелинейную динамику. М.: Едиторал УРСС, 2002.

17. Дубинцев Ю.Н. Колебания и волны. Учебное пособие, Сибирское университетское издательство, Новосибирск, 2004.

18. Манаков С.М. Введение в физику колебаний, Алматы, Казак университетi. 2004.

19. Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. М.: Издательство физ.-мат. литературы, 2002, -292 с.

Дата добавления: 2014-01-11