Адсорбционные равновесия

Лекция 3.

Как уже отмечалось ранее, ПАВы снижают межфазное натяжение благодаря их высокой адсорбционной способности на различных границах раздела фаз. Остановимся подробнее на рассмотрении явления адсорбции и вначале вспомним основные положения, известные Вам из общего курса коллоидной химии.

Адсорбция представляет собой самопроизвольное перераспределение компонентовмеждуобъемной фазой и поверхностным слоем. Компонент системы, который переходит из объема на поверхность, называется адсорбатом; а фаза, формирующая поверхность, - адсорбентом.

Для количественного описания процесса адсорбции применяют две величины. Первая из них называется абсолютнойадсорбцией (А) и представляет собой число молей (граммов) адсорбата, приходящихся на единицу площади поверхности или единицу массы адсорбента. При рассмотрении абсолютной адсорбции используют метод конечной толщины, предложенный Гуггенгеймом. Вторая характеристика адсорбции (Г) определяется избытком числа молей адсорбата в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме объемной фазы, также отнесенным к единице поверхности или массы адсорбента. При рассмотрении этой величины используют метод Гиббса (метод избыточных величин), поэтому величину Г часто называют избыточной (гиббсовской) адсорбцией.

Рассмотрим кратко методы Гуггенгейма и Гиббса, начиная с первого (метод слоя конечной толщины или метод Гуггенгейма).

Рассмотрим простую систему, состоящую из бинарного истинного раствора и твердого адсорбента и находящуюся при постоянной температуре. Для ясности представим себе, что этот бинарный раствор состоит из синего красителя (метиленового голубого) – адсорбата, и воды в качестве растворителя. Понятно, что если краситель растворяется в воде с образованием истинного раствора, то раствор окрашивается в голубой цвет. Введем в этот раствор твердый адсорбент, например, активированный уголь, и оставим полученную систему на некоторое время. После достижения равновесия увидим, что интенсивность окраски раствора уменьшилась– из интенсивно синего раствор стал бледно-голубым. Это значит, что часть красителя перешла из раствора (объемной фазы) на поверхность активированного угля, т.е. произошла адсорбция красителя на поверхности твердого адсорбента. Получим уравнение для расчета величины адсорбции.

Рисунок 1. К расчету абсолютной и гиббсовской адсорбции.

Для этого воспользуемся схемой, которая иллюстрирует описанный выше опыт (рисунок 1). Бинарный раствор красителя в воде обозначим фазой a, твердый адсорбент – активированный уголь – фазой b. По оси ординат будем откладывать концентрацию С моль/л, по оси абсцисс – некоторую координату x, характеризующую изменение свойств системы в зависимости от расстояния от поверхности раздела. Допустим, что на поверхности раздела между раствором и твердым адсорбентом формируется адсорбционный слой, заключенный между x_s и x ^a_s, где x_s – координата, где поверхность твердого адсорбента граничит с поверхностным слоем; x^a_{s –} координата, где поверхностный слой граничит с объемной фазой a. Тогда толщину поверхностного слоя можно обозначить h и выразить как (x_s - x ^a_s). На рисунке сплошной линией показан профиль концентраций компонента С₂ (здесь и далее нижний индекс «2» будет характеризовать все параметры, относящиеся к растворенному веществу, а индекс «1» - к растворителю).

Для простоты допустим, что в процессе адсорбции концентрация адсорбата резко ступенчато возрастает в поверхностном слое, достигнув величины С₂^s . Тогда общее число молей адсорбата (n₂), находящееся в системе, можно вычислить следующим образом:

n₂ = n^as ₂ + n^ss₂ = V_as∙C₂ + V_s∙ C^s₂

где n^as ₂ – число молей адсорбата в объемной фазе (до поверхностного слоя); n^ss₂ – число молей адсорбата в поверхностном слое; V_as – объем фазы a до поверхностного слоя; V_{s –} объем поверхностного слоя. Величина адсорбции представляет собой число молей адсорбата в поверхностном слое, отнесенное к единице площади поверхностного слоя, т.е.:

А = n^ss₂/s = h∙C^s₂ =

Из-за невозможности экспериментального определения объема и толщины поверхностного слоя, метод Гуггенгейма используется только при проведении термодинамических расчетов. Гиббсом был предложен другой метод определения величины адсорбции, который представлен ниже.

При рассмотрении метода Гиббса будем использовать ту же схему, что и для метода Гуггейгейма - тот же бинарный раствор в равновесии с твердым адсорбентом. Гиббс предложил считать, что поверхностный слой не имеет собственного объема и толщины, тогда число молей адсорбата в таком случае можно выразить так:

n₂ = n^a ₂ + n^s₂ = V_a∙C₂ + V_s∙ (C^s₂ – С₂)

Величина n^s₂/s представляет собой избыточную (гиббсовскую адсорбцию), обозначаемую большой греческой буквой гамма - Г. По своему физическому смыслу гиббсовская адсорбция представляет собой избыток числа молей компонента в поверхностном слое определенного объема по сравнению с числом молей компонента в объемной фазе такого же объема. В отличие от величины абсолютной адсорбции, этот избыток можно определить экспериментально, зная исходную концентрацию адсорбата до адсорбции и равновесную концентрацию адсорбата после адсорбции. Зависимость величины адсорбции от равновесной концентрации адсорбата называется изотермойадсорбции.

Сопоставляя эти два метода, можно получить взаимосвязь между абсолютной и гиббсовской адсорбции, а именно:

Из этого простого выражения вытекает несколько важных выводов. Во-первых, гиббсовская адсорбция в отличие от абсолютной может быть отрицательной. Во-вторых, если концентрацией адсорбата в объеме по сравнению с его концентрацией на поверхности можно пренебречь, то величины абсолютной адсорбции и гиббсовской практически совпадают. Те случаи, когда Г<0, здесь рассматриваться не будут; обратим внимание на то, когда А ≈ Г. Это возможно в двух случаях – 1) при адсорбции газов и паров на твердых адсорбентах; 2) при адсорбции поверхностно-активных веществ (ПАВ) из водных растворов.

В заключении вспомним уравнение, связывающее гиббсовскую адсорбцию с величиной межфазного натяжения, называемое фундаментальным уравнением Гиббса:

-ds = S Г_idm_i, где m_I – химический потенциал компонента;

В частности, для бинарного раствора это уравнение переходит в широко используемое уравнение Гиббса для неэлектролитов:

,

где R – универсальная газовая постоянная; Т – температура.

На этом, в основном, заканчивается материал, известный Вам из общего курса коллоидной химии.

Продвинемся немного далее и представим себе, что концентрацию компонентов можно выразить не в моль/л, как ранее, а в мольных долях – (х). Тогда, введя следующие обозначения, получим:

n₀ – общее число моль в системе, n_s – число моль в поверхностном слое, x₀₂ - мольная доля второго компонента до адсорбции, x₂ – равновесная концентрация второго компонента после адсорбции, х₂^s - концентрация второго компонента в поверхностном слое. Для 1 компонента справедливы те же самые обозначения.

Общее число молей в поверхностном слое можно представить как:

n_s = n₁^s+n₂^s ; тогда

Г₂^х =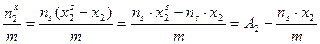

Или:

Г₁^х = , где

А₁ = 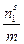; А₂ =

Г₂^х и Г₁^х – величины гиббсовской адсорбции для 2-го и 1-го компонентов, в случае, когда их концентрации выражены в мольных долях.

Вернемся к фундаментальному адсорбционному уравнению Гиббса для бинарного раствора:

-dσ = Г₁^хdμ₁ + Г₂^х dμ₂

и рассмотрим 2 случая:

а) случай предельно разбавленного раствора, когда изменением химического потенциала 1–го компонента (растворителя) можно пренебречь. Тогда:

-dσ = Г₂^х dμ₂

Г₂^х =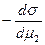

μ₂= μ₂⁰ + RT·x₂

Г₂^х =

б) некоторый искусственный случай, когда разделяющая поверхность (см. лекцию 1) выбирается так, чтобы адсорбция 1-го компонента Г₁ была равно 0, т.е. Г₁ = 0. Для такого случая справедливы следующие обозначения и уравнение:

Г₂¹ = 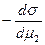= 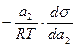, где а₂ – активность второго компонента.

Данное уравнение справедливо для любых концентраций, а не только для предельно разбавленных растворов.

Итак, для бинарных растворов можно записать серию уравнений:

Г₂^v = 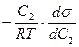(концентрация выражена в моль/л);

Г₂^х = (концентрация выражена в мольных долях);

Г₂¹ = 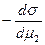= 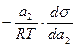(когда Г₁ = 0).

Далее приводится несколько уравнений, позволяющих предсказать вид изотермы гиббсовской адсорбции. Вне зависимости от способа выражения концентраций избыточную гиббсовскую адсорбцию можно обозначить как Г₁^s и Г₂^s для 1-го и 2-го компонентов, соответственно. Тогда опять же для бинарного раствора можно записать:

-dσ = Г₁^σdμ₁ + Г₂^σ dμ₂

Кроме фундаментального адсорбционного уравнения Гиббса применим к бинарному раствору уравнение Гиббса-Дюгема:

Σx_i·dμ_i = 0

Объединив 2 последних уравнения, получаем:

И, наконец:

Учитывая то, что

Г₂¹ = 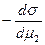, можем записать еще одно уравнение для ее расчета:

Г₂¹ =

Таким образом, величина Г₂¹ определяется однозначно и не зависит от способа выражения концентрации. Мы сами выбираем такое положение разделяющей поверхности, когда Г₁ = 0. Остальные же величины гиббсовской адсорбции не равны между собой, т.е. Г₂^v¹Г₂^х (аналогично и 1-го компонента).

Вернемся опять к мольным долям:

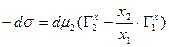
и введем такое ограничение, что

n_s = n₁^s+n₂^s = const,

т.е. число моль в поверхностном слое постоянно (грубо говоря, это означает то, что если в этот поверхностный слой что-то приходит, то что-то должно из него уходить). Тогда:

Г₂^х = -Г₁^х

Запишем без вывода еще несколько уравнений, связывающих между собой Г₂^х, Г₁^х и Г₂¹, не забывая о том, что х₁ + х₂ = 1.

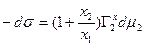
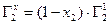
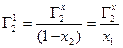
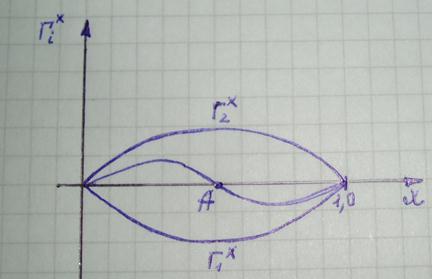
Анализируя совокупность представленных уравнений можно изобразить типичные изотермы гиббсовской адсорбции (рисунок 2), рассчитанные по методу избытков Гиббса.

Рассмотрим граничные области представленных изотерм:

1) При х₂ = 0, Г₂^х = 0, т.е. изотермы всегда выходят из начала координат.

2) При х₂ = 1, Г₂^х = 0

3)0< х₂<1 при 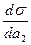<0 Г₂^х>0

при 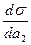>0 Г₂^х<0

4) Г₂^х = -Г₁^х

5) Точка А, где изотерма пересекает ось абсцисс, называется адсорбционной азеотропией, т.е. при таких концентрациях разделение компонентов невозможно.

Рисунок 2. Изотермы гиббсовской адсорбции.

Запишем еще несколько уравнений, связывающих величины Г и А (гиббсовской и абсолютной адсорбции) и часто использующихся при решении задач:

х₂ = и х₁ = ;

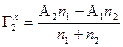
Г₂^х =

Г₂^х =

Наконец, следует упомянуть еще одно выражение:

Р₁Г₁^s + Р₂Г₂^s = 0, где

Р – некоторый параметр, являющийся функцией молярных объемов (V) компонентов. В таком случае последнее выражение можно конкретизировать и записать как:

Для того, чтобы приведенный в этой лекции материал был усвоен Вами хорошо, рекомендуется самостоятельно выполнить приведенные ниже задания.

Дата добавления: 2014-01-11