Ізотерми Ван-дер-Ваальса

Рівняння ізотерми можна отримати, якщо в (6) покласти 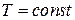. Його можна привести до виразу

.

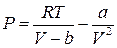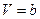Якщо температура велика, то останній доданок можна не враховувати. Ізотерма буде мати вигляд гіперболи із асимптотами (ізобара) і (ізохора).

Для дослідження ізотерм для кожного значення температури перетворимо рівняння (6):

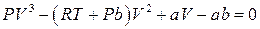. (7)

Це рівняння третьої степені відносно об’єму V і воно має три кореня. Тобто при фіксованих значеннях T і Р речовина може мати три значення об’єму, або, що те ж саме, три значення густини. В окремому випадку, при відповідних значеннях коефіцієнтів в рівнянні (7), всі три кореня будуть рівні. При цьому ліва частина виразу (7) стає точним кубом (V - V ₀)³.

З’ясуємо зміст коренів рівняння Ван-дер-Ваальса. Уявні корені нас не будуть цікавити, оскільки вони не мають фізичного змісту.

На рис. 2 представлені ізотерми Ван-дер-Ваальса і для порівняння приведена ізотерма Ендрюса.

Як видно, ізотерма Ван-дер-Ваальса не співпадає з експериментальною ізотермою Ендрюса: замість прямої ділянки 2 - 4 - 6, що відповідає двофазному стану “речовина-газ”, вона має хвилеподібну ділянку 2-3-4-5-6. При цьому фіксованому значенню тиску, наприклад, P ₁ відповідають три значення молярного об’єму V ₁, V ₂, V ₃. Зрозуміло, що мінімальному з цих значень V ₁ відповідає рідкий стан речовини (гілка 1 - 2 – стиснення рідини), а максимальному V ₃ – газоподібний стан (гілка 6-7 – стиснення газу). А який зміст третього кореню – стану з об’ємом V ₂?

Ділянка 3 - 5 відрізняється від інших тим, що на ній із збільшенням об’єму тиск не спадає, а зростає: . В природі не існує речовин, у яких при зростанні тиску збільшується об’єм, тобто зменшується густина. Можна уявити собі, що такий стан все ж таки реалізувався. Тоді локальне зростання тиску, яке обов’язково буде мати місце в статистичній системі, призведе до зростання об’єму, що в свою чергу призведе до додаткового збільшення тиску, і т.д. поки система не перейде в точку 5, від якої вже починається „нормальна” поведінка системи. З тих же причин будь-яке випадкове мале зменшення тиску призведе до самовільного переходу речовини в стан, що відповідає точці 3. Тобто такий стан абсолютно нестійкий і тому реалізуватись не може.

На ділянках 2-3 і 5-6 з підвищенням тиску об’єм зменшується, і необхідна умова термодинамічної стійкості стану виконана, що, в принципі, припускає можливість реалізації цих станів. За особливих умов ці стани і справді можуть бути реалізованими. Їх називають метастабільними. Ділянка 5-6 зображає пересичену пару, а ділянка 2-3 – перегріту рідину. Ці фази можуть існувати до моменту торкання із іншою більш стійкою за даних умов фазою. Пересичена пара переходить в насичену, якщо з’являється крапля води. Перегріта вода почне інтенсивно кипіти, при попаданні в неї бульбашки повітря.

Експериментально стан пересиченої пари можна реалізувати при швидкому охолодженні закритої посудини з повітрям, що містить водяну пару. Необхідно лише попередньо очистити повітря від слідів пилу і електричних зарядів - центрів конденсації. При цьому після різкого охолодження, а значить, після зменшення пружності насиченої пари, вона все ж таки довгий час не конденсується, залишаючись пересиченою, тобто кількість її молекул більша, ніж це потрібно для насичення.

Стан перегрітої рідини реалізується ще важче. Рідину очищають від домішок і мікроскопічних бульбашок повітря. Останнє досягається в результаті довгого кип’ятіння рідини. Якщо тепер таку рідину нагріти, то вона навіть в умовах переходу з рідкого стану в газоподібний, залишиться рідиною.

Отже, речовина не може перейти з газоподібного стану в рідкий через абсолютно нестійку проміжну область 3-4-5. Дослід показує, що перехід цей здійснюється через двофазний стан, пряма 2-4-5. Тобто кореню V ₂ за даної температури лише при тиску, що дорівнює тиску насиченої пари, відповідає стабільний стан.

Рівноважне значення цього тиску безпосередньо з рівняння Ван-дер-Ваальса не можна знайти. Але його можна визначити з загальних термодинамічних міркувань. Як було показано Максвелом, робота не повинна залежати від того, чи відбувається перехід з рідкого стану до газоподібного по теоретичній ізотермі однорідної речовини 2-3-4-5-6, чи по ізотермі двохфазного стану 2-4-6,

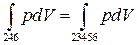
Звідки випливає, що пряму 2-4-6 необхідно провести так, щоб були рівні площі областей під кривою 2-3-4-5-6 і прямою 2-4-6 або, що рівносильно, заштриховані площі на рис. 2.

Значення рівняння Ван-дер-Ваальса полягає, перш за все, в тому, що воно описує факт існування у речовини двох фаз – рідкої і газоподібної. Окрім того, як ми побачимо нижче, з рівняння Ван-дер-Ваальса випливає такий важливий факт, як існування критичної температури і критичного стану взагалі..

Дата добавления: 2014-01-11