Критичний стан та його параметри для газу Ван-дер-Ваальса

Якщо побудувати ізотерми Ван-дер-Ваальса для різних температур, можна побачити, що з підвищенням температури ізотерми розташовуються все вище, а максимуми і мінімуми ізотерм зближуються як по вісі абсцис (зближуються три корені V ₁, V ₂, V ₃), так і по вісі ординат (зменшується відповідна різниця тисків). Нарешті, при T=T_кр всі три корені збігаються між собою V ₁= V ₂= V ₃= V _кр, а максимум і мінімум ізотерми зливаються, перетворюючись у точку перегину. Це означає, що зникає різниця між різними станами речовини, T_кр і є тією температурою, існування якої є характерною властивістю речовини.

Для знаходження критичних параметрів T _кр, р _кр і V _кр, врахуємо, що рівняння (7) переходить в

. (8)

Оскільки в ньому всі три кореня співпадають і рівні V _кр, рівняння повинно приводитись до вигляду

. (9)

Піднесемо його в куб та порівняємо коефіцієнти при однакових степенях. Це дасть три рівняння

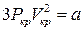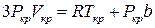, , (10)

Розв’язавши систему (10), одержимо значення критичних параметрів, виражених через стали a і b

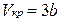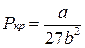, , (11)

Значення критичних параметрів (11) можна отримати і в інший спосіб, врахувавши, що для точки перегину повинні виконуватись умови

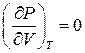та .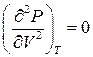

Значення критичних параметрів для деяких речовин

Речовина	T кр, K	Р кр, 10^5Па	V кр, 10^-3м^3/кг
водень (H2)	33,2	13,29	32,26
азот (N2)	126,0	33,93	3,22
кисень (O2)	164,3	50,34	2,32
хлор (Cl2)	417,1	77,08	1,75
водяна пара (H2O)	647,25	220,53	2,50

Рівняння Ван-дер-Ваальса має велике значення, по-перше, тому, що воно якісно вірно описує поведінку речовини при зміні температури, тиску і об’єму а також факт переходу речовини з газоподібного стану в рідкий і навпаки; по-друге, дозволяє оцінити значення температур і тисків, при яких конденсація газів можлива. Іншими словами, рівняння Ван-дер-Ваальса якісно досить добре описує систему рідина-газ, але в кількісному відношенні дає результати, які відхиляються від даних експерименту.

Головні відхилення полягають в наступному:

1. Для даної речовини a і b в рівнянні Ван-дер-Ваальса повинні бути незалежними від температури. Насправді ж для співпадання ізотерм теоретичних і експериментальних при різних температурах доводиться підбирати різні a і b, тобто a = f (T) і b = f (T).

2. З (10) повинно випливати, що критичний коефіцієнт 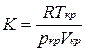рівен

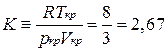
і повинний бути однаковим для всіх речовин. На практиці ж ми для різних речовин отримуємо різні значення. Наприклад, для води 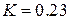, а для гелію . Взагалі-то для легких газів (He, H₂ та ін.) теорія і практика збігаються краще, ніж для важких.

3. Співвідношення V _кр =3 b, отримане з рівняння, не виконується, більш точне V _кр »2 b.

4. В області існування двох фаз рідина-газ рівняння Ван-дер-Ваальса не узгоджується з дослідом.

Теорія Ван-дер-Ваальса має лише якісний характер. Але вона дозволила вперше описати і пояснити широкий клас явищ, пов’язаних з переходами із рідкого стану в газоподібний і навпаки.

4. Закон відповідних станів

Пригадаємо, що ізотерми ідеальних газів не залежать від індивідуальних властивостей газів (якщо ізотерми побудовані для одного моля). Можна і для реальних газів записати рівняння так, щоб воно не залежало від природи газу, тобто було універсальним.

Візьмемо в якості одиниць об’єму, тиску та температури критичні значення цих величин – такі величини називають приведеними

, ,

, , .

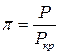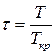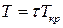Остаточно

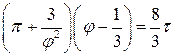. (12)

Це рівняння приймає однаковий для всіх речовин вигляд. Звідси можна зробити висновок, що і поведінка різних речовин повинна бути однаковою. Зокрема, виникає впевненість в тому, що в принципі будь-який газ можна привести в рідкий стан, і можна оцінити температуру і тиск (використовуючи дослідні данні для інших речовин), за яких можлива конденсація газу. (Так було у випадку водню.)

Твердження про еквівалентність поведінки всіх систем рідиа-газ називається законом відповідних станів. Кількісно цей закон формулюється так: якщо два приведених параметра речовин однакові, то і третій параметр також однаковий.

Однак необхідно відзначити, що закон відповідних станів, отриманий з наближення рівняння Ван-дер-Ваальса, не виконується точно реальних газів і рідин.

5. Внутрішня енергія газу Ван-дер-Ваальса

отримаємо спочатку вираз для внутрішньої енергії з молекулярно-кінетичних міркувань. Внутрішня енергія Ван-дер-Ваальса складається з внутрішньої енергії молекул газу і кінетичної енергії руху центру мас молекул, яка в сумі дорівнює C _v T, та з потенціальної енергії взаємного притягівання молекул (в моделі пружних кульок силам притягування не відповідає ніяка потенціальна енергія), яка має від’ємне значення. Підкреслимо, що кінетична енергія руху може бути представлена у вигляді C _v T лише у випадку, коли C _v не залежить від температури,

U = E _k+ E _n (13)

Потенціальна енергія притягування дорівнює роботі, яку необхідно витратити проти сил притягування для того, щоб молекули розвести на нескінченність, коли взаємодією між ними можна знехтувати, а потенціальна енергія взаємодії рівна нулеві. Молекулярний тиск

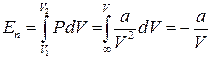. (14)

Нижня границя інтегрування у формулі (14) обрана такою, щоб потенціальна енергія при ньому дорівнювала нулю. Для внутрішньо енергії газу Ван-дер-Ваальса можна записати вираз

(15)

Цю ж формулу можна отримати і термодинамічними методами. Враховуючи, співвідношення 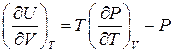, яке можна отримати, використовуючи другий закон термодинаміки, запишемо вираз для диференціала внутрішньої енергії

. (16)

З рівняння Ван-дер-Ваальса випливає, що

(17)

тому

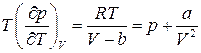(18)

І рівняння (16) набуває вигляду:

(19)

Вважаючи, що U = 0 при Т = 0 і V = ∞, з (19) ми отримаємо:

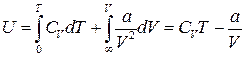, (20)

де C _V не залежить від Т.

Отже внутрішня енергія газу Ван-дер-Ваальса залежить також і від його об’єму U=f (T, V).

Дата добавления: 2014-01-11