Investigation of the system compatibility

Kronecker–Capelli theorem. 1. A linear system (2.1) is consistent if its basic matrix and its augmented matrix have the same rank, i. e. .

A consistent system is determined if the ranks are equal to the unknowns number, i. e. .

2. A consistent system is undetermined if the ranks are less than the unknowns number, i. e. .

3. A linear system is inconsistent if its basic matrix and its augmented matrix have the different rank, i. e. .

If , then carrying out the backward way we obtain the corresponding values of unknowns.

If , then we should choose the main (basic) unknowns, i. e. those ones which coefficients generate the unit matrix. The basic variables are remained on the left, and other variables are transposed to the right parts of equations. The variables placed on the right part of the system are called free variables. The basic variables are expressed through free ones using the backward way. The obtained equalities are the general solution of the system.

Assigning to free variables any numeric values, we can find corresponding values of the basic variables. Thus we can find the particular solutions of the initial system of equations.

If free variables are assigned zero value, then the obtained particular solution is called basic.

If the values of the basic variables are not negative, then the solution is called supporting.

Investigation of the system compatibility is carried out using Gauss method or Jordan–Gauss method.

Example 4. Investigate the compatibility of the given system:

.

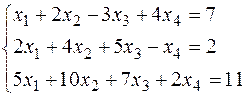Solution. By elementary row operations of the augmented matrix, we obtain:

.

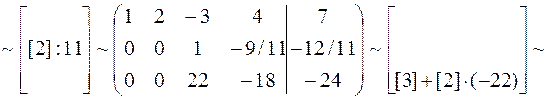
The initial system is equivalent to the following system of equations:

.

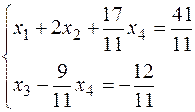Let’s obtain the general solution:

,

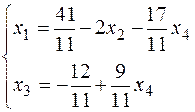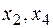where are basic unknowns, are free ones.

For example, obtain the particular solution, if :

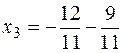or , or .

Thus , , , are the particular solution.

For example, obtain the basic solution, if :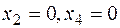

, .

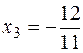Thus , , 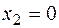, 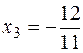are the basic solution.

In this example the basic solution is not the supporting one, because .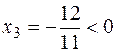

Дата добавления: 2014-01-11