Normal Probability Distributions

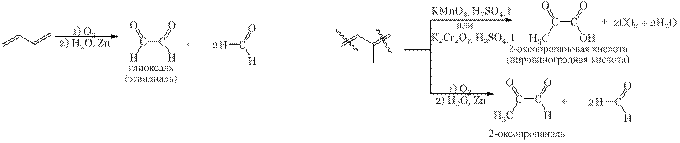
Реакции окисления.

В результате жёского окисления и озонолиза образуется смесь моно- и диальдегидов (или кетокислот).

Introduction to Normal Probability Distributions

Example 1: Understanding Mean and Standard Deviation

1. Which normal curve has a greater mean?
2. Which normal curve has a greater standard deviation?

Example 2: Interpreting Graphs of Normal Distributions

The heights (in feet) of fully grown white oak trees are normally distributed. The normal curve shown below represents this distribution. What is the mean height of a fully grown white oak tree? Explain the standard deviation of the normal distribution.

Example 3: Estimating a Probability for a Normal Curve.

Adult IQ scores are normally distributed with µ = 100 and σ = 15. Estimate the probability that a randomly chosen adult has an IQ between 70 and 115.

Example 4: Determining Intervals

An instruction manual claims that the assembly time for a product is normally distributed with a mean of 4.2 hours and standard deviation 0.3 hours. Determine the interval in which 95% of the assembly times fall.

The Standard Normal Distribution

Example 1: Finding z-Scores

The test scores for a civil service exam are normally distributed with a mean of 152 and standard deviation of 7. Find the standard z-score for a person with a score of:

(a) 161 (b) 148 (c) 152

Example 2: Finding z-Scores ( Try It Yourself)

The mean speed of vehicles along a stretch of highway is 56 mph with a standard deviation of 4 mph. You measure the speed of three cars traveling along this stretch of highway as 62 mph, 47 mph, and 56 mph. Find the z-scores that corresponds to each speed. What can you conclude?

Example3: Finding an x-Value

The test scores for a civil service exam are normally distributed with a mean of 152 and standard deviation of 7. Find the test score for a person with a standard score of

(a) 2.33 (b) -1.75 (c) 0

Example4: Finding an x- Value (Try It Yourself)

The speeds of vehicles along a stretch of highway have a mean of 56 mph and a standard deviation of 4 mph. Find the speeds x corresponding to z-scores of 1.96, - 2.33, and 0. Interpret your results.

Example 5: Using the Standard Normal Table

1. Find the cumulative area for a z -score of -1.25.

1. Find the cumulative area that corresponds to a z-score of 1.15

Example 6: From Areas to z-scores

1. Find the z -score corresponding to a cumulative area of 0.9803

1. Find the z-score that corresponds to a cumulative area of 0.4052.

Example 7: Finding Area under the Standard Normal Curve.

1. Find the area under the standard normal curve to the left of z=-0.99
2. Find the area under the standard normal curve to the right of z=1.06
3. Find the area under the standard normal curve between z=-1.5 and z=1.25.

Applications of Normal Distribution

Example 1: Comparing Scores from two Distributions

The Graduate Record Exam (GRE) and the Miller Analogy Test (MAT) are tests that graduate schools use to evaluate applicants. GRE scores are normally distributed, with µ = 1500 and σ = 300, while MAT scores are normally distributed, with µ=50 and σ=5. You decide to take both tests. You score 1875 on the GRE and 57 on the MAT. On which test did you score better? Explain.

(Tips: 1. Transform each test score to a z-score; 2. Find a percentile for each score; 3. Decide which score is better)

Example 2: Finding Probabilities for Normal Distributions

IQ scores are normally distributed with a mean of 100 and standard deviation of 15. Find the probability that a person selected at random will have an IQ score less than 115.

Example 3: Finding Probabilities for Normal Distributions

Monthly utility bills in a certain city are normally distributed with a mean of $100 and a standard deviation of $12. A utility bill is randomly selected. Find the probability it is between $80 and $115.

Example 4: Finding Percentiles

Monthly utility bills in a certain city are normally distributed with a mean of $100 and a standard deviation of $12. What is the smallest utility bill that can be in the top 10% of the bills?

Example 5: Finding a Specific Data Value

Scores for a civil service exam are normally distributed, with a mean of 75 and a standard deviation of 6.5. To be eligible for civil service employment, you must score inn the top 5%. What is the lowest score you can earn and still be eligible for employment?

Дата добавления: 2014-01-11