Спектральні характеристики періодичних сигналів

Спектр періодичного сигналу є дискретним, оскільки складається з окремих ліній на шкалі частот. Частота першої гармоніки визначається періодом сигналу ω=2п/Т.

Згідно принципу суперпозиції полів та закону збереження енергії, кожна складова спектру переносить певну частину енергії, що передається сигналом вцілому. Оскільки ряд Фур’є є безмежним і він застосовується для представлення прямокутних імпульсів, то зрозуміло, що з підвищенням частоти, енергія кожної гармоніки повинна зменшуватись. Якщо можна представити сигнал з певною точністю (у %) відносно амплітудних значень гармонік або значень енергії сигналу, то такий ряд можна обмежити певним набором частот. Смугу частотного діапазону, в якому набір гармонік із заданим степенем точності відтворює реальний сигнал називають шириною спектру сигналу. Існує загальна закономірність: чим менша тривалість фронту сигналу або менша тривалість імпульсного сигналу, тим більш широкий спектр гармонік необхідно використати для точного відтворення цього сигналу. Для характеристики спектру вводять поняття «спектральної густини сигналу», що характеризує розподіл енергії або потужності в певному діапазоні частот.

В загальному випадку для періодичного сигналу використовують його нормоване представлення x(t) та одиничне навантаження R_н=1Ом.

Тоді енергія і потужність визначаються відповідними інтегралами.

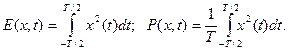
Використовуючи теорему Парсеваля можна виразити сигнал в частотному діапазоні через відповідну залежність в певному часовому інтервалі (-∞;∞).

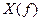- Фур’є образ періодичного сигналу;

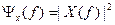- спектральна густина енергії (ESD).

Геометричний зміст її відповідає прямокутнику на частотному спектрі сигналу (розмірність Дж/Гц). Оскільки 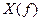- парна функція, то можна записати:

Для періодичного сигналу використовують теорему Парсеваля, аналогічно можна представити спектральний розподіл потужності інформаційного сигналу (PSD).

- коефіцієнти комплексного ряду Фур’є.

Оскільки спектральна густина потужності, як і енергії є дискретною функцією, то її можна представити, використовуючи одиничну δ-функцію:

- властивість δ-функції.

Середнє нормоване значення потужності дійсного сигналу:

- для періодичного сигналу;

- для неперіодичного сигналу.

Автокореляцією називається процес узгодження сигналу зі своєю копією (відбитком), зсуненим на певний час τ.

Спектральні залежності густини енергії та густини потужності є автокореляційними функціями, що кратно повторюються з періодом 2π п.

Властивості автокореляційної функції:

1. R_x(τ) = R_x(-τ) – функція симетрична відносно нуля;

2. R_x(τ) ≤ R_x(0);

3. Автокореляційна функція та густина енергетичного спектру є фур’є образами одне іншого. .

З останньої властивості слідує, що

Такий сигнал називається енергетичним сигналом. Він може бути потужнісним сигналом. Для цього сигналу автокореляційна функція записується як:

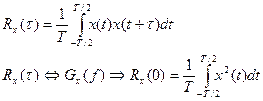
Дата добавления: 2014-01-11