Показатели вариации. П.1.Виды показателей вариации

П.1.Виды показателей вариации

ОПР: Изменение признака под воздействием случайных факторов называется случайной вариацией.

Показатели вариации можно разделить на 3 группы:

1. Показатели центра распределения – среднеарифметическое, мода, медиана.

2. Показатели степени вариации – вариационный размах, дисперсия, коэффициент вариации.

3. Показатели типа распределения – кривые распределения.

М₀ – мода – наиболее часто встречаемое значение.

М_l – медиана – величина изучаемого признака, которая находится в середине упорядоченного ряда.

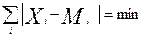
Если в выборке 2m+1 случаев, то М_l = Х _m+1

Если 2m, то М_l = X_m+X _m+1

Если М₀ отражает типичный вариант значения признака, то медиана практически выполняет функцию средней величины для неоднородной совокупности.

ПРИМЕР: Пусть необходимо найти доход группы людей из 100 человек, 99 из которых имеют доход от 100$ до 200$, а месячный доход последнего человека из этой группы составляет 50000$.

№					…….			……
Доход $					…….			…….

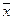≈ 600 – 700$

М_l =163$

Для симметричных распределений 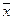= М₀ = М_l

Показатели степени вариаций делят на относительные и абсолютные.

Абсолютные

• Размах вариации R
• Среднее линейное отклонение
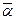
• Дисперсия σ²
• Среднеквадратичное отклонение σ

Относительные:

· Коэффициент вариации V_σ

1. R = X_max - X_min Показывает амплитуду выборок.

К недостаткам R можно отнести тот факт, что очень низкое (высокое) значение признака может быть вызвано какими – либо случайными обстоятельствами‌.

2.

3.

4. 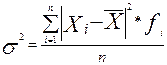- взвешенная дисперсия

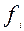- веса каждого варианта

5.

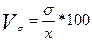
Если V_{σ 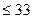,} то выборка считается статистически однородной.

П.2. Вариация альтернативного признака

Энтропия распределения

В ряде случаев возникает необходимость в измерении дисперсии альтернативных признаков, т.е. тех признаков, которыми обладают одни единицы совокупности, а другие единицы совокупности не обладают ими.

Примерами таких признаков являются: ученая степень преподавателя ВУЗа, работа по полученной специальности, бракованная продукция. Значение альтернативного признака обычно задается единицей, если объект этим признаком обладает и нулем, если не обладает.

Пусть р – доля единиц, которые обладают данным признаком, а

q – доля единиц, которые не обладают данным признаком.

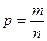, n –объем выборки

1, p

ζ= p+q=1

0, q

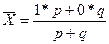
σ² = (1 - p)²p + (0 - p)²q = q²p + p²q = pq(q + p) = pq

p + q

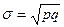
σ²_max = 0,25; 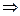σ_max = 0,5

Обобщенной характеристикой различий внутри ряда служит энтропия распределения.

ОПР: Энтропия – мера неопределенности данных наблюдений. Она зависит от числа градации признака и от вероятности каждого из них. Измеряется в битах.

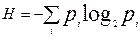
Если все варианты равновероятны, то энтропия максимальна:

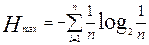
Если признак принимает 2 значения, то для n = 2, Н _max = 1

Относительная энтропия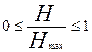

Энтропия часто используется в социальной статистике в качестве меры неопределенности политической ориентации избирателей.

Пример(к зачету): имеются данные о распределении голосовавших в 2-х районах области за кандидатов в местное законодательное собрание.

Партия	Район 1	Район 2
1. Союз правых сил
2. Яблоко
3. Блок Жириновского
4. КПРФ
5. Единство
Итого:

Определить, в каком районе выше степень неопределенности ориентации потребителей.

П.3. Виды дисперсии, в совокупности разделенные на группы

Правило сложения дисперсий

Можно определить 3 показателя вариации признака в совокупности:

1. Общая дисперсия σ₀²

2. Межгрупповая дисперсия σ²

3. Средняя из внутригрупповых дисперсий 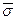²

- Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.

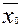. - средняя по всей совокупности;

n_i – кол-во единиц в каждой группе (веса)

- Межгрупповая дисперсия характеризует вариацию изучаемого признака, возникшего под влиянием группировочного признака.

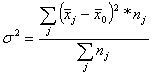
- средняя величина по j-й группе;

- Внутригрупповая дисперсия σ_j² отражает часть вариации, вызванную влиянием неучтенных факторов и независящую от группового признака.

- Средневзвешенная дисперсия:

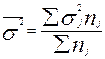
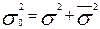- сложение дисперсий.

ПРИМЕР: Распределение торговых предприятий по объему прибыли и формам собственности.

Объем прибыли на 1 предприятие., млрд. руб	Государственные предприятия	Негосударственные предприятия
1,0 -1,2	-
1,2 – 1,4	-
1,4 – 1,6	-
1,6 – 1,8
1,8 – 2,0
2,0 – 2,2
2,2 – 2,4		-
2,4 – 2,6		-
Итого:		-

= 1,8 млрд руб

σ₀² = 89,8 млн руб

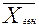= 2 млрд руб; 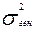=46,8 млн руб

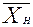=1,628 млрд руб; 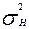=63,6 млн руб

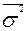= (46,8 +63,6)/2 = 55,3 млн руб

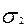=34,5 млн руб

По теореме о сложении дисперсий: 89,8 = 34,5 +55,3

П.4. Эмпирический коэффициент детерминации

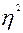показывает, какая доля общей дисперсии приходится на дисперсию, вызванную вариацией группировочного признака.

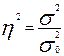
Эмпирическое корреляционное отношение ,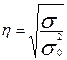

Если 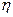= 0, то группировочный признак не влияет на результативный признак.

Если 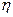= 1, то результативный признак изменяется только под влиянием группировочного признака.

В нашем примере 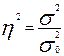= 38,5% (только эта часть вар. обусловлена различиями в форме собственности предприятий).

Дата добавления: 2014-01-11