КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Почленное деление числителя дроби на ее знаменатель
|
|
|
|
З1. Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.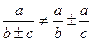
.
Пример 1. Найти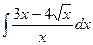 
.
Выполним в подинтегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла
.
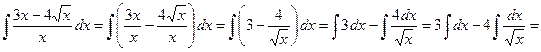
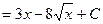З2. Из этого примера видно, что слова “ найти неопределенный интеграл ” означают за счет преобразований подинтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.
33. Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования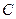 
пишется один раз, так сумма или разность постоянных интегрирования все равно есть постоянная величина.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 12188; Нарушение авторских прав?; Мы поможем в написании вашей работы!