Лекция № 11 “Применение определенного интеграла

Сходимость интеграла, а из расходимости интеграла следует расходимость интеграла.

З3. При исследовании сходимости несобственных интегралов I и II родов чаще всего используют интегралы такого типа, как приведен в Примере 3.

в науке и технике”

1. Работа по сжатию пружины.

Пусть тело массой прикреплено к пружине с коэффициентом упругости 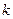. Требуется вычислить работу, которую совершит сила упругости при растяжении пружины от 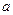до 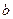(Рис. 13):

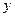
Рис. 13. Вычисление работы упругой

силы.

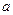
Из физики известно, что сила упругости , а работа 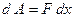. Отсюда находим, что 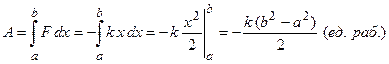. Если выполняется неравенство , то 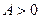, т.е. она совершается против силы упругости. В противном случае работа совершается силой упругости.

2. Работа по откачке жидкости из резервуара.

Пусть резервуар представляет собой параболоид вращения и имеет высоту . Резервуар заполнен жидкостью с плотностью 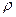. Вычислить работу, которую надо совершить при полной откачке жидкости из резервуара (Рис. 14).

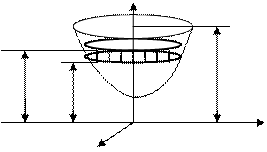
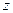
Рис. 14. Вычисление работы по откачке

жидкости из параболоида.

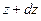
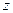
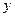
Параболоид вращения задается уравнением 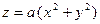. На слой жидкости, расположенный на высоте между 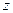и , действует сила тяжести 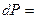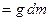, где – ускорение свободного падения, – масса рассматриваемого слоя жидкости. В силу того, что 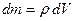(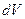– объем рассматриваемого слоя жидкости), то 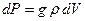. Для тела вращения, которым является резервуар с жидкостью, элемент объема . Работу, которую надо совершить по откачке этого слоя жидкости, равна . Следовательно, работа по откачке всей жидкости из резервуара равна

.

3. Работа по постройке пирамиды.

Пусть необходимо построить пирамиду высотой со стороной основания из материала с плотностью . Требуется найти работу по возведению этой пирамиды (Рис. 15).

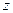
Рис. 15. Вычисление работы по пос-

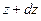тройке пирамиды.

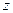
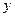
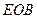Для того чтобы увеличить высоту пирамиды на , надо затратить материал массой . Так как треугольник подобен треугольнику 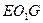, то 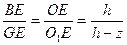. В силу того, что треугольник 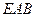подобен тре-угольнику 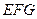, то 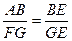. Отсюда следует, что , т.е. 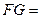. Таким образом, сила тяжести, действующая на выделенный слой материала, будет равна 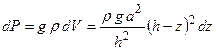. Элемент работы определяется формулой 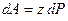. Тогда работа по возведению всей пирамиды будет равна .

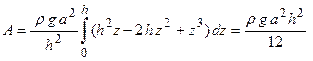4. Давление жидкости на вертикально погруженную стенку.

Пусть в жидкость с плотностью вертикально погрузили пластину. Требуется вычислить давление, оказываемое со стороны жидкости на пластину (Рис. 16).

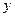
Рис. 16. Вычисление давления жид- 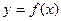кости на вертикально погруженную

жидкость.

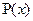Давление на глубине обозначим через , тогда давление в слое жидкости от до будет равно , где 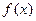– функция, которая опмсывает форму пластины. Отсюда находим давление, оказываемое со стороны жидкости на пластину: .

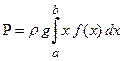Пример 1. Вычислить давление жидкости на пластину, имеющую форму по-луокружности с радиусом 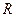, диаметр которой совпадает с поверхностью (Рис. 17).

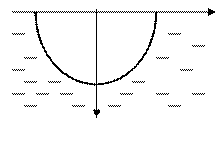
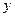
Рис. 17. Вычисление давления жидкости

на пластину, имеющую форму полуок-

ружности с радиусом .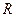

В данном примере 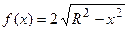, следовательно, давление жидкости на пластину равно . Используя метод замены переменной интегрирования, показать самостоятельно, что давление равно .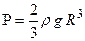

5. Вторая космическая скорость.

Известно, что на любое тело массой , которое находится на высоте над поверхностью Земли, имеющей массу 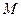и форму шара радиусом 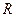, действует сила притяжения Земли , где – гравитационная постоянная. Второй космической скоростью называется такая скорость, при которой тело не возвращается на Землю. Это означает, что телу придается такая кинетическая энергия 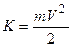(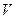– скорость движения), что оно может быть удалено в бесконечно удаленную точку по отношению к Земле. Для того чтобы удалить тело в бесконечно удаленную точку по отношению к Земле, необ-ходимо совершить работу против сил гравитации

.

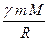Приравнивая полученное выражение для работы значению кинетической энергии, получим выражение для второй космической скорости

.

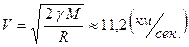6. Численность популяции с перекрывающимися поколениями.

Пусть численность некоторого биологического вида в момент времени 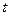равна . Рассмотрим размножение этого вида в условиях неограниченного коли-

чества пищи, отсутствия хищников и конкурентов, а также стихийных катастроф и бедствий. За промежуток времени рождается 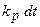(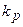– коэффициент рождаемости) особей, а умирает (– коэффициент смертности) особей. Тогда численность популяции изменяется на величину 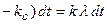, где 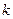– коэффициент пропорциональности. Отсюда следует, что 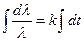. Интегрируя и потенцируя первообразную, получим 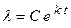. Применим эту формулу для расчета количества людей живущих на Земле. По данным переписи 1950г. их количество составляло 2 млрд. человек, поэтому полученную формулу можно записать в виде 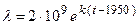. Известно, что каждые 30 лет число людей удваивается, следовательно, 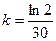. Таким образом, окончательная формула для расчета живущих на Земле людей имеет вид 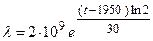. Использование этой формулы показало, что к 2000г. на Земле должно проживать 6 млрд. человек, что практически совпало с данными по международной переписи населения.

Дата добавления: 2014-01-11