Т2. Если функции и линейно-зависимы на сегменте , то на этом отрезке вронскиан тождественно равен нулю

.

Откуда находим 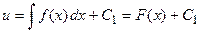. С учетом определения функции 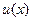вновь получаем ДУ I с разделяющимися переменными: . Разделяя переменные и интегрируя, получим .

З1. Отметим тот факт, что общее решение ДУ II содержит две постоянные интегрирования 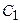и .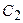

2). ДУ II, явным образом разрешенное относительно второй производной,не содержит неизвестной функции: 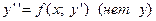. В этом случае производят замену 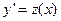и с учетом того факта, что , ДУ II сводится к ДУ I, решение которых было изучено в предыдущих лекциях: .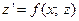

Пример 1. Решить ДУ II .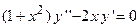

В данном дифференциальном уравнении второго порядка в явном виде отсутствует неизвестная функция 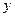, поэтому проведем замену 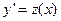и с учетом того факта, что , ДУ II сводится к ДУ I 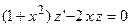, в котором переменные разделяются . Интегрируя это равенство, получим

.

Вновь разделим переменные 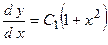; и проинтегрируем полученное равенство .

3). ДУ II, явным образом разрешенное относительно второй производной, не содержит аргумента: 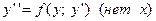. В этом случае производят замену 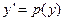и с учетом того факта, что 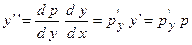, ДУ II сводится к ДУ I: .

Пример 2. Решить задачу Коши: .

Данное уравнение не содержит в явном виде аргумента, поэтому воспользуемся заменой 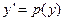. С учетом того факта, что 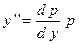, ДУ II сведем к ДУ I: 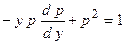. Разделим переменные 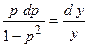, после чего проинтегрируем это равенство . Потенцируя полученное выражение, находим, что . Откуда . Для нахождения постоянной интегрирования воспользуемся начальными условиями, т.е. подставим в найденное равенство , получим . Вновь разделяя переменные, найдем, что 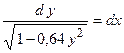. Интегрируя это равенство, получим выражение для искомой функции . 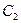Для нахождения постоянной интегрирования воспользуемся начальными условиями, т.е. подставим в найденное равенство , получим 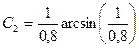. Таким образом, решение задачи Коши после взятия функции синус от обеих частей равенства имеет вид

.

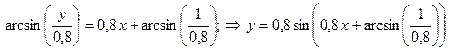2.Линейные ДУ II.

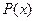О2. Линейным ДУ II называется дифференциальное уравнение второго порядка вида , где , и 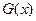– заданные непре-рывные функции или постоянные величины.

О3. Функция 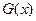называется правой частью линейного ДУ II. Если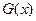 , дифференциальное уравнение второго порядка называется однородным, в противном случае, когда – неоднородным.

Рассмотрим линейное однородное дифференциальное уравнение второго по-

рядка (ЛОДУ II) и выясним структуру его общего решения.

О4. Две функци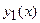и и 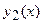называются линейно-зависимыми, если выполняется равенство 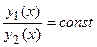, в противном случае эти функции назы-ваются линейно-независимыми.

Т1. Если две линейно-независимые функци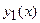и и 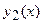являются частными решениями линейного однородного ДУ II, то функция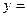 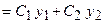также является решением этого уравнения.

О5. Определитель, составленный из частных решений ЛОДУ II 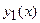и 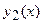и их первых производных, называется определителем Вронского или вронскианом .

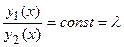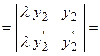
Док-во. Пусть , тогда и . Следовательно, определитель Вронского в соответствии со свойствами определителей (см. Лекцию № 1, Первый семестр).

Т3. Если функци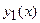и и 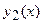два частных решений ЛОДУ II и их определитель Вронского тождественно равен нулю на сегменте 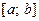, то на этом отрезке функци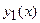и и 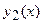линейно-зависимы.

Док-во. Пусть точка 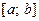, для которо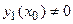й и 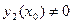. Обозначим отношение 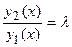, тогда имеет место равенство 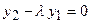. По условию теоремы определитель Вронского 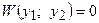,следовательно,

.

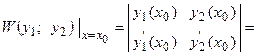
Так как 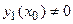, то . Рассмотрим функцию

.

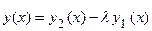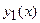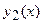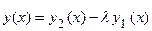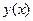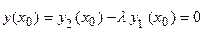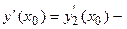
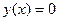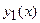Эта функция является решением ЛОДУ II, так как функции и два частных решений ЛОДУ II, а функция – их линейная комбинация. Функция и ее первая производная удовлетворяют нулевым начальным условиям, так как и . Отсюда следует, что , так как решение является единственным решением ЛОДУII, удовлетворяющим нулевым начальным условиям. Отсюда следует, что , т.е. функции и 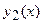линейно-зависимы.

Дата добавления: 2014-01-11