Примеры. Логическое сложение (дизъюнкция)

Логическое сложение (дизъюнкция)

Логическое умножение (конъюнкция)

Логическое умножение есть соединение двух простых высказываний союзом "И". Например, возьмем два высказывания: «Дважды два равно четырем» (a), «Трижды три равно девяти» (a). Сложное высказывание «Дважды два равно четырем и Трижды три равно девяти» истинно, т.к. истинны оба высказывания a и b. Но если взять другие высказывания: «Дважды два равно четырем» (c), и «Стол имеет 2 ножки» (d), то сложное высказывание «Дважды два равно четырем и Стол имеет 2 ножки» будет ложным, т.к. ложно высказывание (d).

Конъюнкция: сложное высказывание, в простейшем случае являющееся соединением двух простых высказываний a и b, истинно тогда и только тогда, когда истинны оба высказывания a и b.

Обозначения операции «конъюнкция»: a & b, a and b, ab, a Λ b.

Знак & - амперсанд - читается как английское "and".

Таблица истинности функции «логическое умножение»:

Логическое умножение
Аргументы	Функция
a	b	F = ab

Пример.

Значение функции a = «2*2=4» =1, значение функции b = «3*3=8» = 0.

Значение функции ab = «(2*2=4) & (3*3=8)» = 0

Логическое сложение есть соединение двух простых высказываний союзом "ИЛИ". Например, возьмем два высказывания: «Дважды два равно четырем» (a), «Трижды три равно девяти» (b). Сложное высказывание «Дважды два равно четырем ИЛИ трижды три равно девяти» истинно, т.к. оно соответствует действительности. Формально, это сложное высказывание является истинным, т.к. истинны оба этих высказывания. С точки зрения здравого смысла, даже если взять два других высказывания: «Дважды два равно четырем» (c) и «Стол имеет 2 ножки» (d), то сложное высказывание «Дважды два равно четырем ИЛИ стол имеет 2 ножки» соответствует действительности и является истинным. Формально оно является истинным, т.к. в этом сложном высказывании есть одно истинное высказывание (c). Таким образом, исходя из обычного смысла союза "ИЛИ", приходим к определению соответствующей логической операции - дизъюнкции.

Дизъюнкция: сложное высказывание, в простейшем случае являющееся соединением двух простых высказываний a и b, истинно тогда и только тогда, когда истинным является хотя бы одно высказывание - a или b.

Обозначения операции «дизъюнкция»: a! b, a or b, a + b, a V b.

Таблица истинности функции «логическое сложение»:

Логическое умножение
Аргументы	Функция
a	b	F = a V b

1. Значение функции a = «2*2=4» =1, значение функции b = «3*3=8» = 0.

Значение функции a V b = «(2*2=4) V (3*3=8)» = 1

2. Значение функции a = «2*2=4» =1, значение функции b = «3*3=9» = 1.

Значение функции a V b = «(2*2=4) V (3*3=9)» = 1

3. Значение функции a = «2*2=5» =0, значение функции b = «3*3=8» = 0.

Значение функции a V b = «(2*2=5) V (3*3=8)» = 0

Равносильные логические выражения: логические функции, представленные разными формулами, но для одинаковых комбинаций логических переменных (аргументов) имеющие одно и то же значение.

Пример. С помощью таблиц истинности определим равносильность двух выражени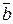й: &и .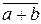

Таблица истинности выражения &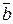
a	b			&

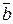
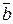
Таблица истинности выражения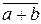
a	b	a+b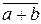

Сравнивая эти две таблицы истинности, можно убедиться в равносильности двух сложных выражений.

Для обозначения равносильных логических выражений применяется знак «=».

Для рассмотренного случая можно записать: &= .

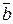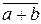Дата добавления: 2014-01-11