Арифметические операции в системе с плавающей точкой

Конечность множества приводит к особенностям машинной арифметики, отличающим ее от обычной известной с первого класса арифметики, законы которой, в общем случае, в не выполняются.

Для двух заданных чисел 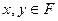результат выполнения арифметических операций (сложения, вычитания, умножения, деления) при вычислении в системе с плавающей точкой будем обозначать: 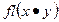. Идеальным для выполнения таких операций является случай, когда сама операция над 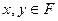выполняется точно, а затем результат либо округляется, либо усекается. Это является основной гипотезой машинной арифметики и реализовано практически на всех ЭВМ.Для выполнения арифметической операции обычно выделяются дополнительные разряды, полученный результат нормализуется, а затем выполняется округление или усечение.

Пример. Пусть - множество чисел с плавающей точкой, для которого 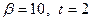. Найдем сумму трех чисел: 0.12+0.17+0.87. Сложение можно провести двумя способами, которые, с точки зрения обычной арифметики, являются эквивалентными: (0.12+0.17)+0.87 или 0.12+(0.17+0.87).

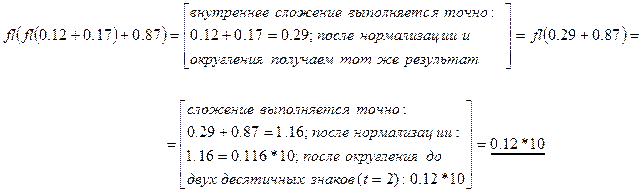
Таким образом, в рассмотренной системе с плавающей точкой (0.12+0.17)+0.87≠ 0.12+(0.17+0.87), что говорит о нарушении сочетательного закона сложения.

В общем случае определение системы чисел с плавающей точкой приводит к тому, что результат арифметического выражения в ней зависит от порядка выполнения операций. Это значит, одному алгоритму, «записанному на бумаге», соответствует множество «машинных» алгоритмов, в каждом из которых другой порядок выполнения действий и, следовательно, может быть другой результат.

При сложении машинных чисел различной величины результат может оказаться точно равен одному из слагаемых. Вполне можно было бы, не изменяя результата, заменить меньшее число нулем. Наименьшее число с плавающей точкой, которое при сложении с числом 1 дает результат, больший, чем 1, часто называется машинным эпсилоном и обозначается 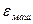. Конкретное значение 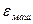зависит от того, какая арифметика используется – с округлением или усечением.

Машинный эпсилон определяет относительную погрешность арифметики компьютера. Если 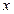и - два положительных числа с плавающей точкой и 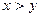, то их сумму можно записать в виде

.

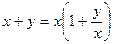Очевидно, что при 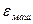сумма с плавающей точкой чисел 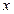и совпадает с 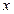. Более тщательные исследования показывают, что относительная погрешность сложения чисел с плавающей точкой ограничена величиной .

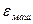Задание. Привести пример системы и двух чисел в ней, для которых результат их сложения точно равен одному из слагаемых.

Важнейшие свойства вычислений с плавающей точкой:

1. Множество чисел с плавающей точкой конечно.

2. Существует наибольшее число с плавающей точкой.

3. Существует наименьшее положительное число с плавающей точкой.

4. Арифметические операции над числами с плавающей точкой не всегда приводят к точно представимым результатам, поэтому результаты приходится усекать или округлять до ближайшего числа с плавающей точкой.

5. Константа 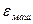есть наименьшее число с плавающей точкой, для которого 1.0+1.0 в арифметике с плавающей точкой. Это число характеризует относительную точность машинной арифметики.

Дата добавления: 2014-01-11