Устойчивость и неустойчивость алгоритмов

Поскольку в системе чисел с плавающей точкой нарушаются основные законы арифметики, то при реализации алгоритмов на ЭВМ большую роль играет порядок организации вычислений, а именно: результат вычислений может сильно зависеть от порядка.

Алгоритм, в котором погрешность, допущенная в начальных данных или допускаемая при вычислениях, с каждым шагом не увеличивается или увеличивается незначительно, называется устойчивым. В противном случае, если погрешность существенно увеличивается от шага к шагу, алгоритм называется неустойчивым.

Чаще всего неустойчивость алгоритма связана с итерационными процессами, когда результат получается посредством последовательности итераций, причем на каждой итерации в качестве исходных данных используются значения, полученные на предыдущей итерации. Существуют неустойчивые алгоритмы, не связанные с итерационными процессами.

Пример. Известно, что ряд Тейлора для функции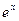

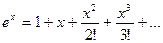
сходится для всех 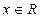. Рассмотрим один из возможных алгоритмов суммирования этого ряда:

Шаг 1. Задать . ; .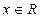

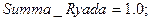
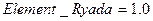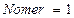Шаг 2.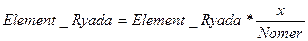

Шаг 3. Если = ,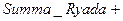

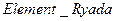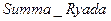то вычисления закончены, результат -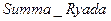

иначе =, ,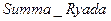

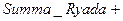
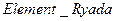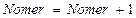переход на шаг 2.

Проверка на шаге 3 учитывает то обстоятельство, что машинная арифметика является приближенной. Выражение 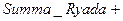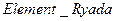будет иметь то же значение, что и 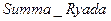, если число 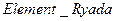достаточно мало. Если провести вычисления по этому алгоритму для различных значений 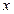, получим числа, представленные в табл.1. Для 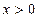эти числа соответствуют истинным значениям, но для картина неудовлетворительная: в некоторых случаях неверны даже знаки результатов. Это говорит о неустойчивости рассмотренного алгоритма.

Таблица1 –

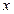
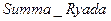
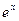
-1 -5 -10 -15 -20	2.718282 148.4132 22026.47 3269017. 4.8516531*10^8 0.3678794 6.7377836*10^-3 -1.6408609*10^-4 -2.2377001*10^-2 1.202966	2.718282 148.4132 22026.46 3269017. 4.8516520*10^8 0.3678795 6.7379470*10^-3 4.5399930*10^-5 3.0590232*10^-7 2.0611537*10^-9

Пример. Необходимо вычислить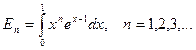

При вычислении интеграла по частям получим:

,

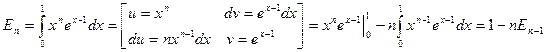т.е. . (10)

Предположим, что вычисления проводятся в системе чисел с плавающей точкой, для которой :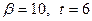

Поскольку для любого 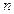при 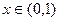: 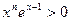, то истинное значение 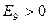. Что привело к ошибке? Единственная ошибка округления, сделанная в приведенных выше вычислениях, - это ошибка в 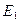, когда 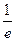округляется до шести значащих цифр. Последующие значения 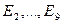получены округлением результатов, вычисленных точно по содержащему ошибку округления значению 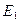. Формула (10) точна для действительной арифметики, следовательно явная ошибка в 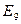всецело обязана ошибке округления в 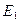. Ошибка в - ,

,

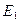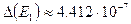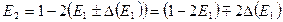т.е. ошибка в 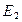― 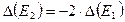. Аналогично, ошибка в 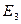― 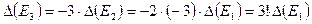и т.д. Ошибка в 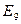― 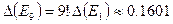. Истинное значение 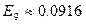. Таким образом, возникающая вследствие неустойчивости алгоритма ошибка – абсолютная погрешность – при вычислении 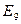значительно больше искомого значения 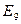, что не даст возможности получить ни одного верного знака в записи числа 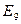, что и наблюдается при вычислении по абсолютно точной с точки зрения обычной арифметики формуле (10).

Преобразуем формулу (10) эквивалентным образом:

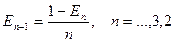. (20)

Теперь на каждом шаге вычислений ошибка в 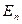умножается на множитель 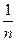. Таким образом, если начать вычисления с некоторого 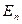для 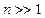и проводить вычисления в обратном порядке, то любая начальная ошибка или промежуточные ошибки округлений будут уменьшаться на каждом шаге, что говорит об устойчивости алгоритма, отвечающего (20).

Оценим значения 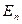в общем виде. Поскольку при 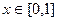: 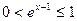, то на сегменте 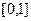: 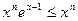, а значит:

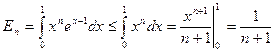, (25)

а это значит, что .

Таким образом, если в качестве стартового значения для вычислений в соответствии с формулой (20) взять, например, 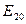, значение которого положить равным нулю

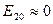, (30)

то начальная ошибка, допущенная при этом в (30), не превосходит в соответствии с (25) 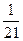. Эта ошибка умножится на 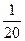при вычислении 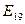, так что ошибка в - .

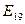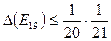Вычисления, проведенные по ормуле (20), приведут к следующему результату:

,

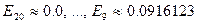что говорит об устойчивости алгоритма (20).

Дата добавления: 2014-01-11