
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нелинейная регрессия. Многие взаимосвязи между экономическими показателями наилучшим образом описываются нелинейными соотношениями
|
|
|
|
Многие взаимосвязи между экономическими показателями наилучшим образом описываются нелинейными соотношениями. Например, зависимость спроса 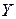 на товар от его цены
на товар от его цены 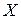 часто представляют как
часто представляют как  , где параметр
, где параметр  .
.
В эконометрике выделяют два класса нелинейных моделей.
К первому относят модели, нелинейные по включенным объясняющим переменным, но линейные по оцениваемым параметрам. Нелинейность по переменным устраняется путем замены переменных. Например, соотношение  относится, очевидно, к этому классу, т.к. оно является нелинейным только по объясняющим переменным. Определим новые переменные как
относится, очевидно, к этому классу, т.к. оно является нелинейным только по объясняющим переменным. Определим новые переменные как  и
и  ; тогда соотношение
; тогда соотношение  , будучи линейным по оцениваемым параметрам, становится линейным и по новым переменным. Если в рассматриваемой модели случайная компонента
, будучи линейным по оцениваемым параметрам, становится линейным и по новым переменным. Если в рассматриваемой модели случайная компонента  является аддитивной, т.е. выражение
является аддитивной, т.е. выражение  изменяется случайным образом путем уменьшения или увеличения на
изменяется случайным образом путем уменьшения или увеличения на  , то модель примет вид
, то модель примет вид  . В таком случае для нахождения оценок ее параметров применим обычный метод наименьших квадратов.
. В таком случае для нахождения оценок ее параметров применим обычный метод наименьших квадратов.
Упражнение 5.1. Исследовалась зависимость между ежегодными транспортными расходами 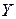 и годовым доходом
и годовым доходом 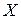 семьи. Были предложены две модели: линейная и квадратичная. Оценивание по данным для 25 семей дало следующие результаты:
семьи. Были предложены две модели: линейная и квадратичная. Оценивание по данным для 25 семей дало следующие результаты:
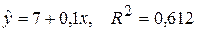 ;
;
 .
.
Какую из построенных моделей следует предпочесть?
Решение. В данном случае предложены две модели с одним и тем же определением зависимой переменной. Поэтому коэффициенты  сравнимы. Результаты оценивания показывают, что линейная функция объясняет 61% дисперсии расходов на транспорт (
сравнимы. Результаты оценивания показывают, что линейная функция объясняет 61% дисперсии расходов на транспорт ( ), в то время как квадратичная зависимость объясняет уже 89% дисперсии переменной
), в то время как квадратичная зависимость объясняет уже 89% дисперсии переменной  . Таким образом, квадратичная функция в наибольшей степени объясняет изменения зависимой переменной и ее следует предпочесть.
. Таким образом, квадратичная функция в наибольшей степени объясняет изменения зависимой переменной и ее следует предпочесть.
Ко второму классу относят модели, нелинейные как по объясняющим переменным, так и по параметрам. Пусть, например, экономическая зависимость моделируется формулой  ,
, 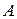 и
и  – параметры модели, подлежащие определению. Модель
– параметры модели, подлежащие определению. Модель  , очевидно, не является линейной как относительно переменной
, очевидно, не является линейной как относительно переменной  , так и параметра
, так и параметра  .
.
В данном случае производная  не будет константой, а будет зависеть от переменной
не будет константой, а будет зависеть от переменной  , что присуще только нелинейным моделям. Параметр
, что присуще только нелинейным моделям. Параметр  определяет эластичность переменной
определяет эластичность переменной  по переменной
по переменной  , т.е. процентное изменение
, т.е. процентное изменение  для данного процентного изменения
для данного процентного изменения  . Действительно,
. Действительно,  , следовательно,
, следовательно,  . Тогда
. Тогда  . Таким образом, параметр
. Таким образом, параметр  показывает на сколько процентов увеличится переменная
показывает на сколько процентов увеличится переменная  , когда значение переменной
, когда значение переменной  увеличится на 1 %. Степенная зависимость
увеличится на 1 %. Степенная зависимость  может отражать, например, соотношение между объемом выпуска продукции
может отражать, например, соотношение между объемом выпуска продукции 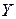 и фактором производства
и фактором производства 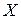 (в этом случае она называется производственной функцией), или же соотношение между спросом на некоторое благо
(в этом случае она называется производственной функцией), или же соотношение между спросом на некоторое благо 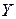 и его ценой
и его ценой 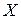 (в этом случае она называется функцией Энгеля).
(в этом случае она называется функцией Энгеля).
Стандартным подходом к линеаризации таких моделей является их логарифмирование.
Действительно,  . Сделаем замену
. Сделаем замену 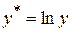 ,
,  и
и  , тогда относительно новых переменных
, тогда относительно новых переменных  и
и  получим линейную модель
получим линейную модель  .
.
Если в рассматриваемой нелинейной модели случайная компонента  является мультипликативной, т.е. она изменяет выражение
является мультипликативной, т.е. она изменяет выражение  в случайной пропорции, то модель примет вид:
в случайной пропорции, то модель примет вид:  . Тогда после логарифмирования модель становится линейной и относительно логарифма случайной компоненты, следовательно, для нахождения оценок ее параметров можно применить МНК. При этом, если случайная величина
. Тогда после логарифмирования модель становится линейной и относительно логарифма случайной компоненты, следовательно, для нахождения оценок ее параметров можно применить МНК. При этом, если случайная величина  имеет нормальный закон распределения, то для анализа качества модели можно использовать
имеет нормальный закон распределения, то для анализа качества модели можно использовать 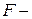 и
и 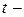 статистики.
статистики.
Если в рассматриваемой модели случайная компонента является аддитивной, т.е.  , то применять обычный метод наименьших квадратов уже невозможно. В таком случае применяют специальные итерационные процедуры.
, то применять обычный метод наименьших квадратов уже невозможно. В таком случае применяют специальные итерационные процедуры.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 314; Нарушение авторских прав?; Мы поможем в написании вашей работы!