Применение фиктивных переменных в регрессионном анализе

При проведении регрессионного анализа часто случается, что отдельные факторы, включенные в модель, являются качественными, и, следовательно, не измеряются в числовой шкале. Один из возможных подходов к решению таких задач – учет влияния качественных факторов посредством введения фиктивных переменных. В качестве фиктивных переменных чаще всего используются булевы переменные, которые принимают только два значения: “0” или “1”. Пусть, например, требуется исследовать зависимость рыночной цены квартиры 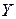в городе Самара не только от ряда количественных факторов 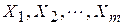, но и от качественного фактора – месторасположения продаваемой квартиры 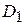. Качественный признак 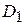указывает на то, расположена ли квартира достаточно близко к историческому центру города, или же она находится на окраине города. Регрессионная модель цены квартиры может быть записана в виде:

где

Если , то свободный член регрессии равен , если же 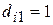, то свободный член регрессии станет 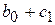. Коэффициенты уравнения 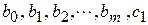можно оценить по МНК. Если МНК-оценка окажется статистически значимой, то можно считать, что цена за квартиру в центре города в среднем на выше, чем на окраине при неизменных значениях других факторов, включенных в модель.

Если качественный признак имеет 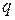уровней (т.е. количество его различных качественных состояний равно 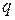), то число булевых переменных в модели следует взять равным 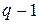. Например, месторасположение продаваемой квартиры можно описать 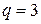уровнями: первый уровень означает, что квартира находится в центре города; второй уровень – на окраине; третий уровень – в пригороде. 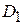В этом случае следует ввести булевых переменных: и 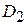. Регрессионная модель цены квартиры примет вид:

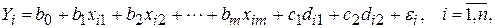
где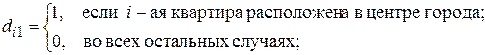

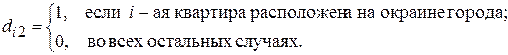
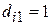Если -ая квартира расположена в центре города, то это будет отражено следующей парой значений фиктивных переменных: и ; если же -ая квартира расположена на окраине города, то это будет отражено такой парой значени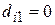й: и ; а если -ая квартира расположена в пригороде, то 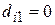и .

Пример 5.1. Требуется исследовать зависимость рыночной цены на квартиру 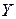(тыс. у.е.) от общей площади 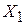(м²), количества комнат 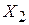и удаленности квартиры от центра города 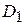. Исходные данные приведены в табл. 5.1.

Таблица 5.1

Исходные данные

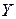
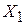
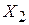
№ наблюдения				Месторасположение квартиры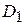
	18,6			окраина
				центр
	14,8			окраина
				центр
				центр
	49,5			центр
	28,5			окраина
	24,7			окраина
				окраина
	33,5			окраина
	88,6	128,4		центр
				окраина
				центр
	73,5			окраина
				окраина

Решение. Необходимо исследовать влияние количественных факторов 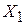и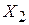и качественного фактора 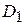- месторасположения квартиры на рыночную стоимость квартиры .

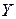В качестве отправной точки выберем модель, содержащую только количественные факторы:

.

Оценивание регрессии по МНК дает следующий результат:

.

Во второй строке приведены стандартные ошибки коэффициентов регрессии, а в третьей строке 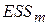– остаточная сумма квадратов, найденная для модели с объясняющими переменными, и коэффициент детерминации . Видно, что только коэффициент при переменной 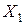можно считать статистически значимым.

Далее будем исследовать влияние качественного фактора –месторасположения продаваемой квартиры на ее цену. Предположим, что фактор “месторасположение” может сказаться только на “начальной” цене квартиры (свободном члене). Тогда модель примет вид:

,

где 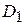– фиктивная переменная, т.е. искусственно введенная переменная, которая принимает значение 1, если наблюдение относится к центру города, и 0, если наблюдение относится к окраине города. В табл. 4.5 показано, как вычислялись значения переменной 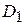по 15 наблюдениям.

Оценивание регрессии по МНК дает следующий результат:

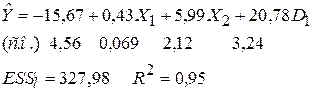
Во второй строке приведены стандартные ошибки коэффициентов регрессии, а в третьей строке 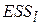- остаточная сумма квадратов, найденная для модели с 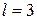объясняющими переменными, и коэффициент детерминации . Видно, что все эмпирические коэффициенты уравнения можно считать статистически значимыми. В частности, и коэффициент при фиктивной переменной также является статистически значимым (наблюдаемое значение - статистики для него составляет 6,4). Другими словами, средняя цена за квартиру значимо выше (на 20,78 тыс у.е.), если квартира находиться в центре города, при неизменных значениях других факторов, включенных в модель.

Полученное эмпирическое уравнение регрессии можно переписать в виде:

,

,

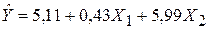где первая строка относится к центру города, а вторая – к окраинам.

Рассмотрим, привело ли включение фиктивной переменной к значимому повышению объясняющей способности уравнения регрессии. Остаточная сумма квадратов с независимыми переменными составляет 1550,997, а с включением фиктивной переменной и 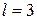. Согласно (4.17) соответствующая 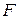- статистика имеет вид:

распределена с 1 и 11 степенями свободы и превышает критическое значение 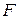, равное 9,65 при 1%-ом уровне значимости.

Таким образом, при добавлении фиктивной переменной наблюдается значительное улучшение в объяснении дисперсии зависимой переменной. Спецификация модели в целом улучшилась – коэффициент детерминации увеличился с 0,76 до 0,95.

Дата добавления: 2014-01-11