Нелинейная регрессия

Применение фиктивных переменных в регрессионном анализе

В модели

Способы уменьшения (устранения) мультиколлинеарности

ЛЕКЦИЯ №5. НЕКОТОРЫЕ АСПЕКТЫ ПОСТРОЕНИЯ МОДЕЛЕЙ

МНОЖЕСТВЕННОЙ РЕГРЕССИИ

ПЛАН

5.1. Явление мультиколлинеарности. Признаки присутствия
мультиколлинеарности в модели

5.1. Явление мультиколлинеарности. Признаки присутствия
мультиколлинеарности в модели

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Мультиколлинеарность означает наличие линейной зависимости между факторными признаками в модели. Линейная взаимосвязь между признаками может проявляться как в функциональной, так и в статистической формах.

Если между объясняющими переменными существует линейная функциональная связь, то ранг матрицы 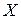становится меньше числа оцениваемых по МНК параметров модели, т.е. , что нарушает условие 6 теоремы Гаусса-Маркова. В этом случае матрица будет иметь линейно зависимые столбцы, а ее определитель станет равным нулю. Следовательно, вычисление наилучшего вектора оценок по формуле (3.5) будет невозможным. Для устранения мультиколлинеарности такого вида следует исключить из модели ту объясняющую переменную, которая связана линейной зависимостью с другими объясняющими переменными.

Однако чаще всего линейная связь между объясняющими переменными носит статистический характер, что проявляется в значительной коррелированности факторных признаков. В этом случае вектор МНК-оценок формально может быть вычислен по формуле: , но определитель матрицы становится близок к нулю. Поскольку дисперсии оценок 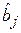пропорциональны диагональным элементам обратной матрицы (см. формулы 4.6), то близость к нулю определителя матрицы 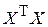может привести к резкому увеличению дисперсий 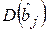. В результате появляются следующие признаки присутствия явления мультиколлинеарности в модели: оценки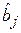 могут иметь большие стандартные ошибки, малую значимость, в то время как модель в целом остается значимой. Как следствие, МНК-оценки параметров модели становятся статистически неустойчивыми: небольшие изменения в исходных данных (например, урезание или добавление небольшой порции исходных данных) могут привести к значительному изменению значений оценок . 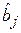При этом возможно как появление неверного знака у оценок 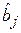, так и появление неожиданно больших (с точки зрения экономической теории) значений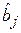 . В результате модель становится непригодной для анализа и прогнозирования.

5.2. Способы уменьшения (устранения)
мультиколлинеарности в модели

Одним из распространенных способов уменьшения (устранения) мультиколлинеарности в модели является отбор факторов в модель на основе анализа матрицы парных коэффициентов корреляции. Для этого используют матрицу парных коэффициентов корреляции:

Заметим, что эта матрица является симметричной, т.к. и , а на главной диагонали ее стоят единицы, т.к. .

Отбор факторов в модель на основе анализа матрицы парных коэффициентов корреляции осуществляется по следующему алгоритму: в модель включают только те факторы из , которые наиболее сильно связаны с зависимой переменной 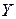, но при этом слабо связаны с другими объясняющими переменными. При этом связь между объясняющими переменными считается сильной, если парный коэффициент корреляции между ними больше числа 0,8 по абсолютной величине.

Другим способом устранения (уменьшения) мультиколлинеарности является пошаговый отбор в модель наиболее информативных переменных. Суть его состоит в следующем. Пусть имеются признаки мультиколлинеарности в модели, содержащей набор объясняющих переменных 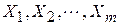. На первом шаге в модель вводят ту объясняющую переменную из , которая имеет с зависимой переменной 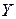максимальный коэффициент детерминации.

На втором шаге в модель включается новая объясняющая переменная, которая вместе с выбранной на первом шаге переменной составляет пару, имеющую с переменной 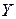наиболее высокий коэффициент детерминации. Таким образом, на втором шаге в модель отбирают двойку наиболее информативных объясняющих переменных.

На третьем шаге в модель отбирают тройку наиболее информативных переменных, включающую в себя результаты выбора на предыдущих шагах, и т.д.

Такие действия по включению новых переменных в модель следует повторять до тех пор, пока для отобранных переменных будет увеличиваться скорректированный коэффициент детерминации. Результирующая модель будет содержать набор наиболее информативных объясняющих переменных и иметь максимальный скорректированный коэффициент детерминации.

Рассмотренные выше способы устранения мультиколлинеарности могут дать разные наборы объясняющих переменных, которые следует включить в модель. Это объясняется тем, что такие пошаговые процедуры присоединения-удаления переменных гарантируют лишь получение близкого к оптимальному набора переменных, следовательно, получаемые с помощью разных пошаговых процедур наборы переменных не обязательно совпадают.

Дата добавления: 2014-01-11