В этой формуле тензор устанавливает соответствие в 4-пространстве между векторными полями и

Скалярное произведение 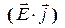в формуле (8) есть работа, совершаемая полем над зарядами в единичном объеме в единицу времени, т.е. мощность механических сил. Следовательно, в записанном в инвариантной форме выражении (9) пространственная часть 4-плотности силы Лоренца определяет скорость изменения количества движения единицы объема, а временная часть - скорость изменения механической энергии единицы объема. Иными словами, составляющие 4-плотности силы Лоренца определяют пространственные и временные производные некоторой величины с размерностью плотности энергии.

Пункт 2. Электромагнитный тензор энергии-импульса

Исключим из выражения (9) с помощью уравнений (5.6) составляющие 4-плотности тока 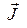и получим выражение для 4-плотности силы Лоренца в виде

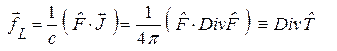. (10)

Правая часть (10) представляется в виде 4-дивергенции симметричного 4-тензора второго ранга 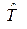(см. Приложение к § 6), называемого электромагнитным тензором энергии-импульса. Компоненты этого тензора 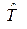имеют вид

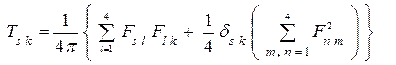. (10*)

Используя определения (5.4), компоненты электромагнитного тензора энергии-импульса (11) можно явно выразить через поля и представить 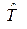в виде

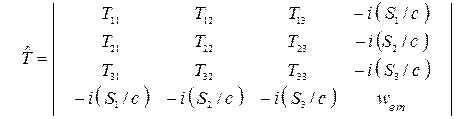, (11)

где представлены компоненты симметричного тензора максвелловских натяжений

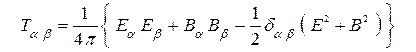, (12)

компоненты вектор Пойнтинга

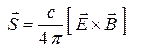(13)

и плотность энергии электромагнитного поля

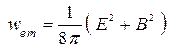(14)

Одним из инвариантов электромагнитного тензора энергии-импульса является сумма его диагональных элементов (след)

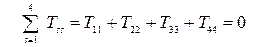. (15)

Как отмечалось выше, в СТО происходит объединение величин, которые втрехмерных представлениях были независимыми. У свободной частицы энергия и импульс объединились в один 4-вектор. Энергия и импульс электромагнитного поля также входят в одно единое образование 4-тензор второго ранга, в который, кроме энергии (скаляра в трехмерном случае) и импульса (вектор в трехмерном случае), входит еще и трехмерный тензор натяжений Максвелла.

В формуле (10) тензор 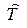устанавливает соответствие в 4-пространстве между векторными полями 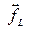и оператора дифференцирования.

Пункт 3. Закон сохранения энергии.

Законы сохранения импульса и энергии являются просто интегралами по трехмерному объему от правой и левой частей соотношения (10), определяющего связь компонент 4-плотности силы Лоренца и компонент тензораэнергии-импульса.

Рассмотрим вначале четвертую составляющую 4-плотности силы Лоренца и четвертую компоненту правой части выражения (10) в виде

.

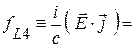
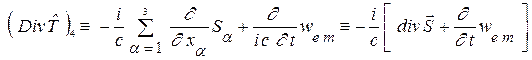Образуем из этого соотношения дифференциальную форму теоремы Пойнтинга

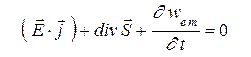. (16)

Интегрируя выражение (16) по объему и отмечая, что 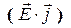характеризует изменение механической энергии заряженных частиц, получим закон сохранения энергии в виде

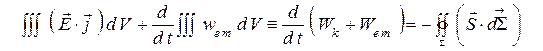, (17)

где 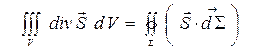и – полная электромагнитная энергия в объеме 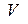. Если система замкнутая или пр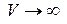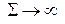и, и 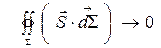система заряженных частиц становится замкнутой, то энергия сохраняется:

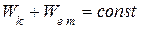. (17)¢

Пункт 4. Закон сохранения импульса.

Получим аналогичным образом выражение для закона сохранения импульса. Рассмотрим пространственную компоненту 4-плотности силы Лоренца

.

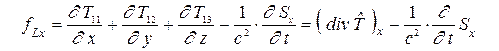Каждую из пространственных компонент умножим на свой орт и, сложив, получим

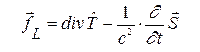. (18')

Проинтегрируем (18') по объему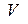

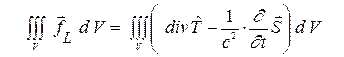(18)

и учтем, что

.

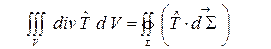1) Плотность силы Лоренца 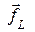равна изменению плотности механического импульса 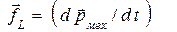, поэтому 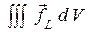можно заменить на

.

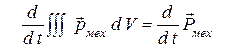2) Введём величину

,

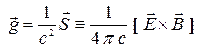которая имеет размерность плотности импульса и называется плотностью электромагнитного импульса, а также интегральную величину

,

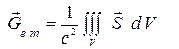называемую импульсом электромагнитного поля в объеме 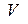1).

Подставляя все в (18), получим закон сохранения импульса в виде

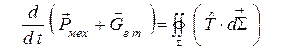. (19)

Если система замкнутая (или 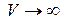,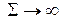), то 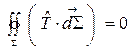и тогда имеет место закон сохранения полного импульса

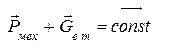. (19)¢

Другая интерпретация закона (19¢) – в отсутствие натяжений импульс сохраняется.

Приложение

Приведем доказательство того, что при учете однородных уравнений Максвелла (5.7) выражение (9) можно представить в форме (10). Используя суммирование по повторяющемуся индексу, преобразуем левую часть (10) к виду

.

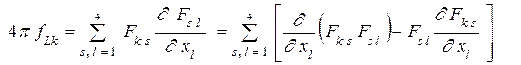В силу полной антисимметричности матрицы { 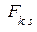} справедливо соотношение 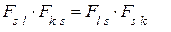, которое позволяет представить второе слагаемое как

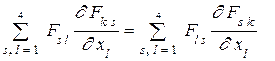
Далее заметим, что в последней сумме можно заменить индексы 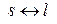. Т огда получим вначале

,

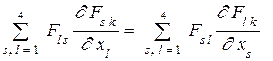а затем в силу полной антисимметрии матрицы { 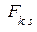} представим последнюю сумму в виде

.

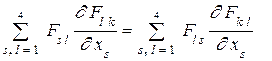Теперь примем во внимание две последние суммы, приравняем их и получим

.

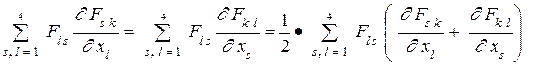Далее учтем уравнения Максвелла в форме

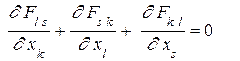
и тогда получим

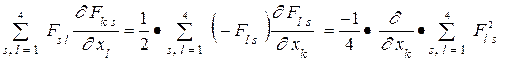
В результате имеем формулу (10) в виде

.

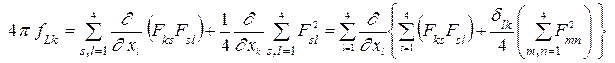1) Вектор Пойтинга должен удовлетворять лишь уравнению (16), поэтому его определение в виде не является однозначным. Однако оно не ведет ни к каким противоречиям и является наиболее плодотворным. Поскольку, то тензор T_ab определен неоднозначно. К его компонентам можно добавить A_ab такие, чтобы. Однако эта неоднозначность устраняется в теории поля требованием, чтобы натяжения давали не только правильную равнодействующую силу, но и правильный вращательный момент.

Аналогичным образом можно решить вопрос с однозначностью в четырех- мерном случае. По необходимо найти момент и потребовать его однозначного определения с помощью тензора T_ik.

Дата добавления: 2014-01-11