Стійкість за Пуассоном

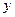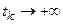Точка фазового простору називається – граничною точкою фазової траєкторії , якщо можна вказати таку послідовність моментів часу , що .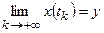

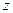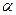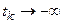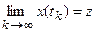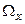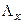Аналогічно, точка називається – граничною точкою, якщо можна вказати таку послідовність моментів часу , що . Множина всіх – граничних точок називається - граничною множиною даної траєкторії, а множина всіх 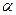– граничних точок 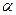– граничною множиною. Траєкторія називається стійкою за Пуассоном, якщо кожна її точка є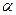- граничною та 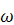- граничною, тобто .

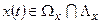Щоб усвідомити значення введеного поняття, помітимо, що будь-який стійкий режим коливань нелінійних дисипативних систем представляється траєкторіями, стійкими за Пуассоном. Це відноситься й до динамічного хаосу, пов'язаному з існуванням дивного аттрактора – режиму, в якому можна вважати стійким в часі його усереднені статистичні характеристики.

З іншого боку, зворотне твердження невірно – не всяка стійка за Пуассоном траєкторія представляє режим динаміки, що з фізичної точки зору може вважатися стійким. Справа в тому, що сама по собі властивість стійкості за Пуассоном ще нічого не говорить про те, як поводяться сусідні траєкторії – чи притягаються вони до вихідної траєкторії або йдуть від неї.

Однак траєкторії, що відповідають перехідним процесам, не є стійкими за Пуассоном.

Обговоримо кілька прикладів. Найпростіший приклад – це стан рівноваги. Йому відповідає фазова траєкторія, що складається з однієї точки, і вона, мабуть, стійка за Пуассоном.

Якщо розглядається траєкторія, відмінна від нерухомої точки, то стійкою за Пуассоном вона буде в тому випадку, якщо має властивість повертатися в як завгодно малу околицю кожної своєї точки нескінченне число раз. Повернення траєкторії в 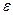- околицю довільно обраної на ній початкової точки називають поверненням Пуанкаре.

Розглянемо замкнуту траєкторію – граничний цикл. Повернення Пуанкаре будуть фіксуватися періодично, з як завгодно високою точністю (рис. 1,а). Час повернення Тє просто період циклу й він не залежить від вибору 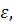принаймні, коли 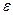стає досить малим.

Звернемося до наступного за ступенем складності прикладу й припустимо, що для будь-якого заданого 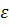можна вказати період повернення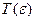однаковий для будь-якої точки старту на даній траєкторії, причому при 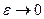цей період прагне до нескінченності (рис. 1,б). Іншими словами, повернення з даним ступенем точністю відбуваються один за одним регулярно, із правильною періодичністю, але період збільшується, якщо ми хочемо збільшити точність вимірювання початкових умов. Такі рухи називають квазіперіодичними. Зокрема, до них відноситься суперпозиція двох періодичних коливань з частотами, які знаходяться в ірраціональному відношенні.

Нарешті, динамічний хаос – це така ситуація, коли повернення Пуанкаре в 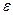- околі стартової точки не проявляють регулярності, інтервал часу між двома послідовними поверненнями виявляється щораз іншим і виникає деякий статистичний розподіл часів повернення (рис. 1,в).

Зі сказаного ясно, що вивчення статистики повернень Пуанкаре – потужний засіб аналізу й класифікації динамічних режимів. Очевидно, потенційні можливості цього підходу ще не повністю вичерпані в сучасній нелінійній динаміці.

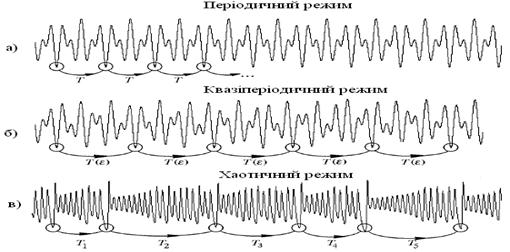
Рис. 1. Повернення Пуанкаре.

Дата добавления: 2014-01-11