Игровые деревья. Принцип минимакса

Существенно другой разновидностью метода ветвей и границ является метод, встречающийся при построении деревьев игр.

Рассмотрим детерминированую игру, в которой игроки делают ходы поочередно. Детерминированность игры определяется следующими моментами:

1. Определена исходная позиция (в картах или домино это не так).

2. Оба игрока имеют полную информацию о текущей позиции (снова в картах или домино это не выполняется).

3. Ходы делаются в пределах правил, но по желанию игроков (в нардах и других играх с костями это не так).

Примерами детерминированных игр являются шашки, шахматы, крестики-нолики.

Пусть имеется некоторая позиция. Как определить, какой ход лучший? Очевидно, нужна какая-то оценка позиций, получающихся в результате сделанного хода. Например, в шахматах оценка позиции должна учитывать материальое соотношение фигур, защищенность короля, наличие проходных пешек и т. п.

Оценка может быть статической и динамической, которая учитывает возможные ответы противника. Динамическая оценка более точная. Например, можно взять незащищенного ферзя, а в ответ получить мат в два хода.

Возможное течение игры можно представить деревом. Корнем дерева является исходная или текущая позиция. Сыновьям корня соответствуют позиции, получающиеся после сделанного хода. Каждая из таких позиций порождает новое множество позиций, получающихся после ответа противника и т. д. Листьям дерева соответствуют конечные позиции (в шахматах мат, пат, теоретически ничейные позиции и т. п.). Листья располагаются на разных уровнях дерева.

Назовем игроков ПЛЮС и МИНУС. Выбор хода каждого игрока соответствует выбору одного из сыновей вершины, которая описывает текущую позицию. В дереве игры уровни вершин, в которых выбираются ходы игроков ПЛЮС и МИНУС, чередуются. Рассмотрим простейший способ построения оценочной функции позиций с точки зрения одного из игроков, например, игрока ПЛЮС.

Присвоим листьям, соответствующим выигрышным позициям, оценку +1, ничейным 0, проигрышным -1. Пусть некоторая вершина дерева A, сыновями которой являются только листья, соответствует ходу игрока ПЛЮС. Очевидно, он должен выбрать одного из сыновей с масимальным значением оценки, поэтому примем это максимальное значение в качестве оценки вершины A. Отцовская для A вершина B соответствует ходу игрока МИНУС. Поскольку оценки в листьях устанавливались для игрока ПЛЮС, игрок МИНУС должен наоборот выбирать сына с минимальной оценкой, предполагая, что его противник сделает лучший ход, то есть оценкой вершины B станет минимум оценок сыновей. В этом и состоит принцип минимакса. Он получен в предположении, что каждый игрок стремится к наивысшему результату при условии наилучших ходов противника.

Таким образом, корень дерева получит оценку +1, 0 или –1, что предопределяет результат игры. На практике все обстоит сложнее. В большинстве игр дерево настолько велико, что не поддается подобным расчетам. Например, в шахматах белые могут сделать 20 вариантов первого хода, на каждый из которых может быть 20 вариантов ответа противника, то есть после полного первого хода может получиться 400 различных позиций. Приходится дерево игры строить не до конечных позиций, а в листьях прибегать к статической оценке. С каждым сделанным ходом дерево достраивается вниз. Чем глубже строится дерево игры и чем точнее статические оценки, тем сильнее игрок, будь то человек или программа. Шахматист применяет неявные статические оценки, используя теорию, интуицию, пристрастие к определенным позициям, антипатии противника по отношению к некоторым позициям и т. п.

Рассмотрим простой пример игры в крестики-нолики на поле 3*3. Игроки поочередно ставят крестик либо нолик в клетках поля. Выигрывает тот, кто получит 3 крестика либо нолика подряд по горизонтали, вертикали либо диагонали.

Построим сначала статическую оценочную функцию. Пусть M – сумма числа строк, столбцов и диагоналей, которые при данной позиции теоретически могут быть заняты игроком КРЕСТИК, а N – аналогичная величина для игрока НОЛИК. Примем за оценку позиции значение F = M – N.

Например, для позиции

+

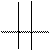игрок КРЕСТИК потенциально может занять строки 2, 3, столбцы 1, 3 и обе диагонали, то есть M = 6, а игрок НОЛИК может занять строки 1, 3 и столбцы 1, 3, то есть N = 4. Таким образом, позиция оценивается величиной F = M – N = 2.

Можно проверить, что если придерживаться принципа минимакса, пользоваться описанной функцией оценки и строить дерево игры на свой ход и ответ противника, то есть на 2 уровня, то первый ход игрока должен быть сделан в центр поля. Для игрока КРЕСТИК этот ход имеет оценку 1, тогда как ход в угол поля оценивается величиной –1, а ход в середину крайней строки или столбца величиной –2.

Описанная функция оценки далеко не всегда соответствует лучшему ходу. Пусть, например, в позиции, соответствующей корню дерева, очередь хода за игроком КРЕСТИК. В скобках проставлены оценки позиций после возможных ходов.

+ 0

+

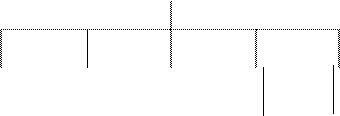+ 0 + + 0 + 0 + 0 + 0

+ + + + + + + +

0 0 + 0 + 0 0

Дата добавления: 2014-01-11