Плоскость в пространстве

Пусть в пространстве задана точка 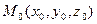и линейно независимые векторы и 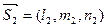. Множество точек , координаты которых удовлетворяют системе уравнений:

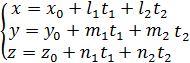(4.1)

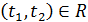
называется плоскостью, проходящей через точку параллельно векторам и 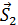. Рассмотрим геометрическую интерпретацию формулы (1). Перенесем начало векторов и 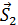в точку и проведем через точку пересекающиеся прямые 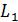и 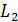в направлении векторов и 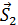. Как известно из геометрии, через две прямые можно провести только одну плоскость. Координаты точек этой плоскости вычисляются по формуле (4.1), которую называют параметрическим уравнением плоскости.

Запишем формулу (4.1) в эквивалентной векторной форме: 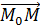=+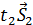. Это уравнение означает, что вектор 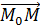есть линейная комбинация векторов и 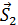а, следовательно, соотношения (4.1) можно написать в виде:

(4.2)

(определитель равен нулю, т.к. его первая строка является линейной комбинацией второй и третьей строк).

Из элементарной геометрии известно, что через три точки 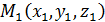, , , 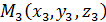лежащие на одной прямой, можно провести плоскость и причем только одну.

Найдем уравнение этой плоскости. Для этого возьмем точку 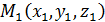и построим векторы 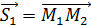и . Эти векторы линейно независимые (не коллинеарные), т.к. точки 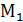, 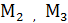не лежат на одной прямой. Уравнение плоскости, проходящей через точку 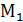, параллельно вектoрам 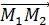и имеет вид:

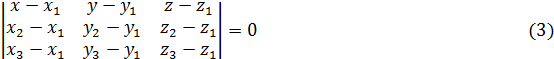(4.3)

(уравнение плоскости, проходящей через три точки , ).

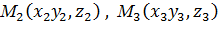Пусть плоскость пересекает координатные оси соответственно в точках 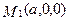, , 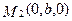(плоскость отсекает от осей отрезки 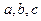) Тогда ее уравнение по формуле (4.3) имеет вид:

.

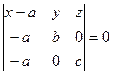Раскрывая определитель, имеем: .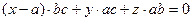

Разделив это уравнение на abc, получаем уравнение плоскости в отрезках на осях:

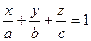(4.4)

Из уравнений (4.2), (4.3) и (4.4) видно, что зависимость между координатами текущей точки 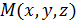линейная.

Так, раскрывая определитель (4.2) по элементам первой строки получаем:

,

Где ; ; 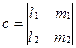. Вектор =(a,b,c) перпендикулярен вектору 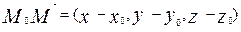, т.к.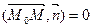

в силу (4.2). Докажем, что множество точек является плоскостью, если координаты этих точек удовлетворяют линейному уравнению

(4.5)

.

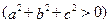Действительно, пусть, например, 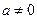, тогда уравнение (4.5) можно решить относительно x: .Введем вспомогательные переменные параметры и . Тогда получим систему уравнений, эквивалентную исходному уравнению

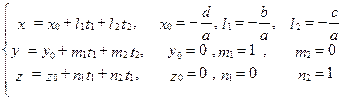
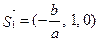Это параметрическое уравнение плоскости, проходящей через точку параллельно векторам и 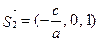Выражение (4.5) называют общим уравнением плоскости.

Пусть 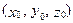- частное решение уравнения (4.5), тогда

.

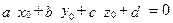Вычитая это равенство из уравнения (4.5), получаем

(4.6)

Обозначим и 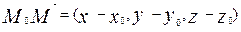- текущий вектор данной плоскости с началом в точке . Из условия (4.6) следует, что , т.е. 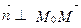. Отсюда следует, что - нормальный вектор плоскости (4.5). Формулу (4.6) называют уравнением плоскости, проходящей через точку А (x ₀, y ₀, z ₀), перпендикулярно вектору .

Пример 4.6.

а) Записать уравнение плоскости в параметрической форме, если она проходит через точку М ₀(1,0,-1) и параллельно векторам , .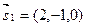

Решение. Подставляя координаты точки М ₀ и координаты векторов , 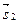в формулу (4.1), получаем:

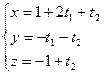
б) Записать общее уравнение плоскости, проходящей через точку М ₀(1,0,-1) и параллельно векторам , .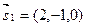

Решение. Подставим координаты точки М ₀ и координаты векторов , 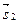в формулу (4.2):

.

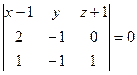Раскрывая определитель, получаем:

.

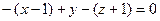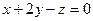- общее уравнение данной плоскости.

Пример 4.7. Записать уравнение плоскости, проходящей через точку A (1; 2; 3) перпендикулярно вектору = (2; −1; 3).

Решение.

Уравнение плоскости имеет вид a (x − x ₀) + b (y − y ₀) + c (z − z ₀) = 0, т.е.

2(x − 1) − (y − 2) + 3(z − 3) = 0, 2 x − y + 3 z − 9 = 0.

Пример 4.8. Записать уравнение плоскости, проходящей через точки A (2; 1; 3), B (−1; 2; 5), C (3; 0; 1).

Решение.

Уравнение плоскости по формуле (4.3) имеет вид

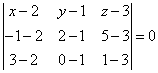
Раскрывая определитель, получаем: 2 y − z + 1 = 0.

Пример 4.9. Составить уравнение плоскости в отрезках на осях, если эта плоскость пересекает оси координат в точках А (3,0,0), В (0,-4,0), С (0,0,5).

Решение.

Плоскость отсекает отрезок а = 3 от оси Ох, отрезок b = -4 от оси Оy и c = 5 от оси Оz. По формуле (4.4) ее уравнение имеет вид:

.

Расстояние точки М ₁(x ₁, y ₁, z ₁) от плоскости ax + by + cz + d = 0 вычисляется по формуле:

.

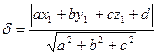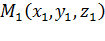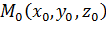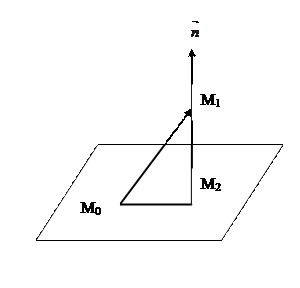
Действительно, пусть - точка вне плоскости и - точка на данной плоскости, 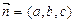- вектор нормали данной плоскости. Тогда (см. рис. 4.6):

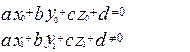
Рис. 4.6. Расстояние от точки до плоскости

Расстояние от точки до плоскости 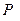равно длине перпендикуляра 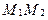, опущенного из точки на плоскость .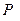

,

,

.

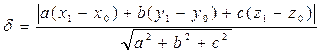Так как , то .

Пример 4.10. Найти расстояние от точки A (2; 3; 1) до плоскости x + y + z = 1.

Решение.

Имеем:

.

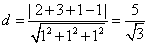4.3. Взаимное расположение в пространстве двух плоскостей:

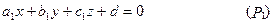
определяется их нормальными векторами и .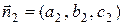

1) Углом между плоскостями a ₁ x + b ₁ y + c ₁ z + d ₁ = 0 и a ₂ x + b ₂ y + + c ₂ z + d ₂ = 0 называется угол j, образованный векторами нормалей и 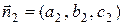к этим плоскостям:

.

2) 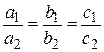– условие параллельности плоскостей a ₁ x + b ₁ y + c ₁ z + + d ₁ = 0 и a ₂ x + b ₂ y + c ₂ z + d ₂ = 0.

3) a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0 – условие перпендикулярности плоскостей a ₁ x + b ₁ y + c ₁ z + d ₁ = 0 и a ₂ x + b ₂ y + c ₂ z + d ₂ = 0.

Это условие может быть записано в более компактном виде: 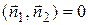, где и 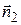векторы нормалей к соответствующим плоскостям.

Пример 4.11. Найти угол между плоскостями x + 2 y – 2 z + 5 = 0 и x + y – 9 = 0.

Решение. Так как , ,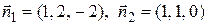

, ,

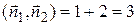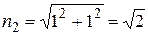то .

Следовательно, угол между плоскостями .

Пример 4.12. Написать уравнение плоскости, проходящей через точку А (–1, 3, 5) параллельно плоскости 3 x + 2 y – z – 5 = 0.

Решение. Вектор нормали заданной плоскости , очевидно, будет вектором нормали и искомой плоскости. Поэтому, используя уравнение плоскости, проходящей через данную точку, получаем:

3(x + 1) + 2(y – 3) – 1(z – 5) = 0 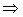3 x + 3 + 2 y – 6 – z + 5 = 0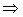

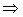3 x + 2 y – z + 2 = 0 – уравнение искомой плоскости.

Дата добавления: 2014-01-11