
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямая в пространстве. Уравнение прямой
|
|
|
|
Множество точек 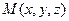 в трехмерном пространстве, координаты которых удовлетворяют системе уравнений
в трехмерном пространстве, координаты которых удовлетворяют системе уравнений
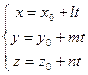
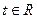 (4.7)
(4.7)
называется прямой, проходящей через точку 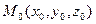 и параллельной вектору
и параллельной вектору 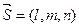 . Вектор
. Вектор 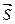 называется направляющим вектором данной прямой, переменная величина
называется направляющим вектором данной прямой, переменная величина 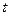 ,
, 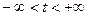 , называется параметром, а система (4.7) называется параметрическим уравнением прямой в пространстве. Параметр
, называется параметром, а система (4.7) называется параметрическим уравнением прямой в пространстве. Параметр 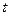 выражается линейно через текущие координаты
выражается линейно через текущие координаты  точки
точки  ,если
,если 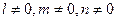 :
:
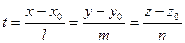
Каноническими уравнениями прямой называют линейные зависимости между координатами точки 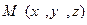 , расположенной на прямой:
, расположенной на прямой:
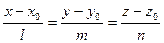 . (4.8)
. (4.8)
Известно из геометрии, что через две точки  и
и 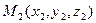 можно провести только одну прямую. Найдем уравнение этой прямой. Очевидно, прямая проходит через точку
можно провести только одну прямую. Найдем уравнение этой прямой. Очевидно, прямая проходит через точку  параллельно вектору
параллельно вектору 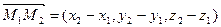 . По формуле (4.8) уравнение прямой, проходящей через две точки
. По формуле (4.8) уравнение прямой, проходящей через две точки 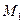 и
и  имеет вид:
имеет вид:
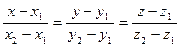 (4.9)
(4.9)
Прямую можно рассматривать как пересечение двух плоскостей 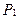 и
и 
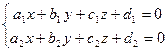 (4.10)
(4.10)
Эта система называется общими уравнениями прямой.
Направляющий вектор 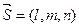 этой прямой перпендикулярен нормальным векторам
этой прямой перпендикулярен нормальным векторам 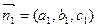 и
и  плоскостей
плоскостей  и
и  . Поэтому, можно выбрать в качестве направляющего вектора векторное произведение нормальных векторов плоскостей:
. Поэтому, можно выбрать в качестве направляющего вектора векторное произведение нормальных векторов плоскостей: 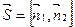 . Координатами точки
. Координатами точки 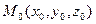 на прямой может служить любое частное решение системы (4.10). Таким образом, по общим уравнениям прямой (4.10) можно составлять канонические уравнения прямой
на прямой может служить любое частное решение системы (4.10). Таким образом, по общим уравнениям прямой (4.10) можно составлять канонические уравнения прямой
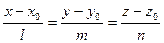
Заметим, что из каждого вида уравнений прямой в пространстве можно получить любой другой вид уравнений прямой в пространстве.
Пример 4.13. Написать уравнения прямой, проходящей через точку А(2,-1,4) параллельно вектору 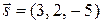 в параметрической и канонической формах.
в параметрической и канонической формах.
Решение. Параметрическое уравнение прямой имеет вид:
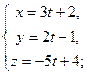
Канонические уравнения прямой имеют вид: 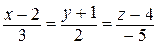 .
.
Пример 4.14. Написать уравнения прямой, проходящей через точку А (– 3, 1, 2) параллельно прямой:
а) 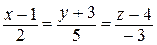 ; б)
; б)  в)
в) 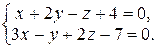
Решение. а) Направляющий вектор заданной прямой 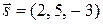 , очевидно, является направляющим вектором искомой прямой. Поэтому:
, очевидно, является направляющим вектором искомой прямой. Поэтому:  – искомое уравнение.
– искомое уравнение.
б) Направляющий вектор заданной прямой  . Следовательно, уравнения искомой прямой
. Следовательно, уравнения искомой прямой  .
.
в) Направляющим вектором искомой прямой будет вектор 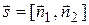 , где
, где 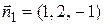 и
и  – векторы нормалей к плоскостям x + 2 y – z + 4 = 0 и 3 x – y + 2 z – 7 = 0.
– векторы нормалей к плоскостям x + 2 y – z + 4 = 0 и 3 x – y + 2 z – 7 = 0.
Тогда  .
.
Поэтому, уравнения искомой прямой: 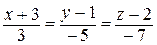 .
.
Пример 4.15. Написать уравнения прямой, проходящей через точки А (2, 3, – 5) и В (– 3, 1, 4).
Решение. Используя уравнения прямой, проходящей через две точки получаем:  .
.
Пример 4.16. Написать канонические уравнения прямой
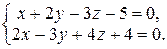
Решение. Найдем направляющий вектор данной прямой
 .
.
Чтобы написать канонические уравнения прямой необходимо еще найти какую-нибудь точку на этой прямой. В качестве такой точки А (x 0, y 0, z 0) возьмем, например ту, у которой z 0 = 0, т. е. А (x 0, y 0, 0). Тогда ее координаты x 0 и y 0 обязаны удовлетворять уравнениям:
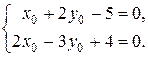
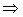

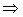

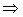

Следовательно, точка А (1, 2, 0) принадлежит заданной прямой. Теперь напишем канонические уравнения этой прямой:
 .
.
Расстояние от точки до прямой в пространстве
Расстояние δ от точки М 1(х1, y1, z1) до прямой L:

равно длине перпендикуляра М 1 М 2, проведенного из точки М 1 на прямую L (рис. 4.7).
Отрезок М 1 М 2 является высотой параллелограмма, построенного на векторах 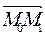 и
и 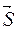 с общим началом в точке М 0(х0, y0, z0).
с общим началом в точке М 0(х0, y0, z0).
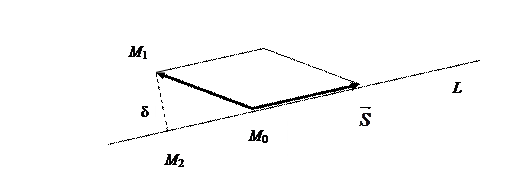
Рис. 4.7. Расстояние от точки до прямой
Площадь этого параллелограмма с одной стороны равна произведению высоты на основание:  , а с другой – по свойству векторного произведения
, а с другой – по свойству векторного произведения  - его длине:
- его длине: 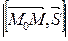 . Отсюда:
. Отсюда:
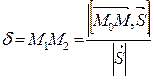 ;
;
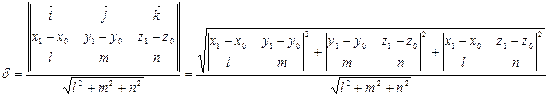 (4.11)
(4.11)
Пример 4.17. Найти расстояние от точки A (4; 4; 4) до прямой L, заданной каноническими уравнениями
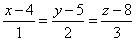 .
.
Решение.
1 способ. Запишем параметрические уравнения прямой L с начальной точкой P (4; 5; 8) и направляющим вектором 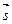 = (1; 2; 3):
= (1; 2; 3):
x = 4 + t, y = 5 + 2 t, z = 8 + 3 t.
Таким образом, проекция точки A на прямую L имеет вид
B (4 + t, 5 + 2 t, 8 + 3 t).
Чтобы найти t, необходимо воспользоваться условием ортогональности векторов 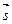 и
и 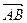 .
.
Имеем
(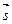 ,
,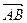 ) = ((1; 2; 3), (t, 1 + 2 t, 4 + 3 t)) = t + 2 + 4 t + 12 + 9 t = 14 + 14 t = 0.
) = ((1; 2; 3), (t, 1 + 2 t, 4 + 3 t)) = t + 2 + 4 t + 12 + 9 t = 14 + 14 t = 0.
Отсюда t = −1, B = (3; 3; 5), 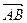 = (−1, −1, 1). Окончательно, имеем
= (−1, −1, 1). Окончательно, имеем 
 .
.
2 способ. По формуле (4.11) получаем:
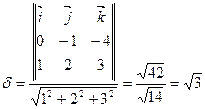 .
.
Скрещивающиеся прямые
Найдем расстояние между двумя скрещивающимися прямыми L 1 и L 2:
 ,
, 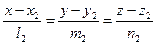 .
.
Расстоянием между прямыми называют длину общего перпендикуляра.
Геометрическое построение общего перпендикуляра начнем с простого примера двух параллельных прямых L 1 и L 3 (рис. 4.8):
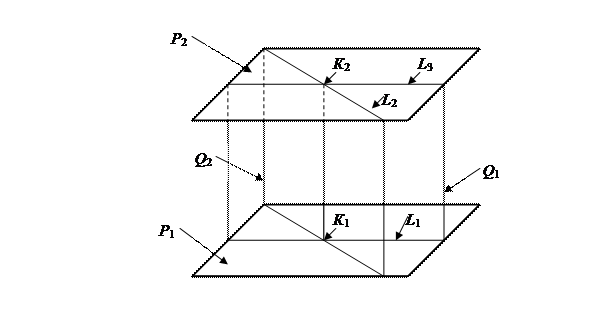
Рис. 4.8. Прямые: параллельные и скрещивающиеся
Возьмем любую точку К 1 на прямой L 1 и в плоскости, проходящей через параллельные прямые L 1 и L 3, проведем перпендикуляр К 1 К 2 к прямой L 3. Это общий перпендикуляр к прямым L 1 и L 3 в силу их параллельности.
Будем считать, что прямые L 1 и L 3 расположены в параллельных плоскостях Р 1 и Р 2, проходящих через точки К 1 и К 2, перпендикулярно вектору 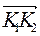 . Проведем в плоскости Р 2 через точку К 2 прямую L 2, пересекающую прямую L 3 . Тогда К 1 К 2 - общий перпендикуляр скрещивающихся прямых L 1 и L 2. Заметим, что длина перпендикуляра К 1 К 2 равна расстоянию между параллельными плоскостями Р 1 и Р 2. Уравнение прямой К 1 К 2 задается пересечением плоскостей Q 1 и Q 2, проходящих через прямые L 1 и L 2, перпендикулярно плоскостям Р 1 и Р 2.
. Проведем в плоскости Р 2 через точку К 2 прямую L 2, пересекающую прямую L 3 . Тогда К 1 К 2 - общий перпендикуляр скрещивающихся прямых L 1 и L 2. Заметим, что длина перпендикуляра К 1 К 2 равна расстоянию между параллельными плоскостями Р 1 и Р 2. Уравнение прямой К 1 К 2 задается пересечением плоскостей Q 1 и Q 2, проходящих через прямые L 1 и L 2, перпендикулярно плоскостям Р 1 и Р 2.
Теперь рассмотрим любые две скрещивающиеся прямые L 1 и L 2. Сначала построим их общий перпендикуляр.
Проведем плоскость Р 1 через прямую L 1 параллельно прямой L 2 и плоскость Р 2 - через прямую L 2 параллельно прямой L 1. Направляющие векторы прямых 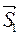 и
и 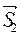 образуют направляющее векторное пространство параллельных плоскостей Р 1 и Р 2.
образуют направляющее векторное пространство параллельных плоскостей Р 1 и Р 2.
Далее, через прямую L 1 и прямую L 2 проведем плоскости Q 1 и Q 2, перпендикулярные плоскостям Р 1 и Р 2. Прямая, задаваемая пересечением плоскостей Q 1 и Q 2, перпендикулярна параллельным плоскостям Р 1 и Р 2. Отрезок К 1 К 2, заключенный между плоскостями Р 1 и Р 2, является общим перпендикуляром скрещивающихся прямых L 1 и L 2. Его длина равна как расстоянию между прямыми L 1 и L 2, так и расстоянию между плоскостями Р 1 и Р 2.
Для нахождения длины общего перпендикуляра прямых L 1 и L 2 построим параллелепипед по трем векторам 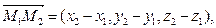
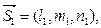
 с общим началом в точке М 1.
с общим началом в точке М 1.
Основание параллелограмма с вершиной в точке М 1 расположено в плоскости Р 1, а основание с вершиной в точке М 2 в плоскости Р 2. Оба основания построены по векторам 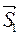 и
и 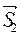 . Поэтому площадь параллелограмма в основаниях равна длине вектора
. Поэтому площадь параллелограмма в основаниях равна длине вектора 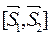 :
:
 .
.
Объем параллелепипеда определим по смешанному произведению векторов 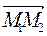 ,
, 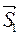 и
и 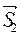 .
.
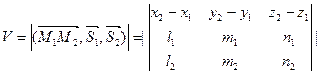 .
.
Расстояние между плоскостями Р 1 и Р 2 равно высоте рассмотренного выше параллелепипеда и может быть вычислено по формуле 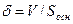 .
.
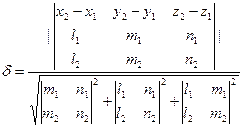 .
.
Уравнения общего перпендикуляра скрещивающихся прямых задаются пересечением плоскостей Q 1 и Q 2, проходящих соответственно через прямые L 1 и L 2 перпендикулярно параллельным плоскостям Р 1 и Р 2:
|
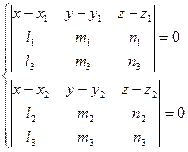

Направляющими векторами плоскостей Q 1 и Q 2, соответственно, являются пары 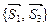 и
и 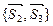 , где
, где  - нормальный вектор плоскостей Р 1 и Р 2.
- нормальный вектор плоскостей Р 1 и Р 2.
Нормальные векторы плоскостей Q 1 и Q 2 определяются векторными произведениями 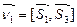 и
и 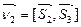 .
.
Пример 4.18. Составить уравнения общего перпендикуляра к скрещивающимся прямым
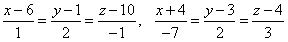
и найти расстояние между ними.
Решение.
Плоскость, параллельная обеим прямым, перпендикулярна вектору:
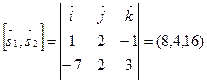 .
.
В качестве нормали этой плоскости можно взять вектор  =(2; 1; 4) коллинеарный
=(2; 1; 4) коллинеарный  . Общий перпендикуляр к данным прямым представляет собой пересечение плоскостей
. Общий перпендикуляр к данным прямым представляет собой пересечение плоскостей
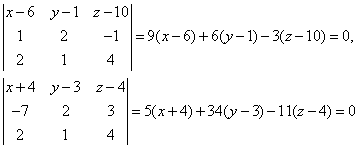
или, после упрощения,
3 x − 2 y − z − 6 = 0, 5 x + 34 y − 11 z – 38 = 0.
Отсюда получаем  - уравнение общего перпендикуляра.
- уравнение общего перпендикуляра.
Далее,
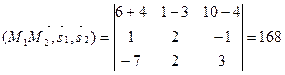 ,
,
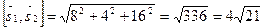 ,
,
 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 5482; Нарушение авторских прав?; Мы поможем в написании вашей работы!