Завдання 3

Частина устаткування виробничої дільниці з часом виходить з ладу і ремонтується. Відмови устаткування, як і терміни ремонту – випадкові величини. Коли ремонтна бригада вільна, вона відразу приймається за роботу, а коли ремонтники зайняті, устаткування чекає своєї черги. Доки устаткування знаходиться в ремонті, або очікує ремонту, випуску продукції на ньому не відбувається і загальне виробництво зменшується. Необхідно визначити, яка середня продуктивність ділянки у даних умовах і які міри потрібні для її підвищення. Отже, потрібно знайти оптимальне співвідношення витрат, що пов’язані з очікуванням ремонту, і витратами на збільшення ремонтних бригад.

Рішення.

Аналітично відомі інтенсивність потоку відмов устаткування l і інтенсивність потоку обслугування m за зміну. Відомі також втрати в одиницю часу: від простою устаткування – n умовних одиниць, на утримання однієї бригади - m умовних одиниць.

Менеджерів, які організують виробничий процес, цікавить середній час очікування обслугування і середній час обслугування при різній кількості ремонтних бригад s. Також важливо знайти оптимальну кількість ремонтних бригад з урахуванням витрат у одиницю часу на простої і на утримання бригади.

1) Розрахуємо показники роботи СМО з одним каналом обслуговування.

При роботі однієї бригади дану задачу можна представити у вигляді одноканальної системи обслугування з необмеженною чергою.

r = l / m.

При r > 1 черга росте необмежено.

При r < 1 маємо такі показники.

Ймовірність відсутності черги:

p₀ = 1 - r.

Ймовірність черги з k замовлень:

p_k+1 = r ^k+1 (1 - r) або p_k+1 = r ^k+1 p₀.

Середній час очікування в системі:

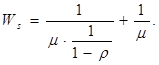
За результатами розрахунків:

2) Розрахуємо показники СМО для s ремонтних бригад та приймемо рішення про їх оптимальну кількість з урахуванням витрат на простої – n грн в одиницю часу і на утримання бригади – m грн в одиницю часу).

Якщо працює s бригад задачу можна описати як багатоканальну систему з необмеженою чергою.

Значення r / s може бути більше за 1.

Якщо r / s ³ 1, тоді черга зростає до нескінченності.

Якщо r / s < 1, то існують фінальні ймовірності.

Ймовірність відсутністі черги:

Середня кількість устаткування у черзі:

Cередня кількість устаткування в системі обслуговування W_s=W_q+1/m. Домножимо ліву і праву частину рівняння на l, отримуємо:

L_s = L_q + r.

Середній час перебування устаткування у черзі:

W_q = L_q / l.

Середній час перебування устаткування в системі:

W_s =(1 / l) L_s.

Припустимо, що витрати в одиницю часу на простой складають 7 умовних одиниць, і на утримання однієї бригади - 5 умовних одиниць. Тоді отримуємо такі результати при різній кількості бригад (припустимо, що l = 1.6, m = 0.9, r = 1.77).

Аналіз результатів. За результатами розрахунків бачимо, що при s = 2: W_s = 17.43, загальні витрати V=7×17.43 + 5×2 = =131.99 у.о.

При s = 3: W_s = 1.5, загальні витрати V=7×1.5 + 5×3=25.54 у.о.

При s = 4: W_s = 1.18, загальні витрати V=7×1.18+5×4=28.24у.о.

Бачимо, що з економічної точки зору вигідно тримати три ремонтні бригади.

7. Література

1. Большаков А.С. Моделирование в менеджменте. Учебное пособие. –М.: Информационно-издательский дом «Филин», Рилант, 2000. - 464 с.

2. Математические методи и модели в планировании у управлении: Сборник задач / С. А. Кулиш, С. А. Воловельская, А.И. Жилин, А. С. Пилипенко. – К.: Вища шк. Головное изд-во, 1985. – 239 с.

3. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров: Учеб.пособ. – М.: Финансы и статистика, 1999. – 656с.

4. Таха Х. Введение в исследование операций: В 2-ч книгах, Кн. 2. Пер. с англ. –М.: Мир, 1985. – 496 с.

Зміст

1.	Вступ....................................................................
2.	Використання теорії масового обслуговування у керуванні виробництвом......................................
2.1.	Системи масового обслуговування з відмовами............................................................
2.1.1.	Одноканальні системи масового обслуговування...................................................
2.1.2.	Багатоканальні системи масового обслуговування.....................................................
2.2.	Системи масового обслуговування з очікуванням.............................................................
3.	Практичне застосування теорії масового обслуговування......................................................
4.	Завдання до лабораторних робіт.........................
5.	Приклад виконання лабораторної роботи №1.....
6.	Приклад виконання лабораторної роботи №2....
7.	Література...............................................................

Дата добавления: 2014-01-11