Вираз зі змінною і його область визначення

Алгебраїчним виразом називається запис, який складається з чисел, позначених цифрами чи буквами і з‘єднаних знаками дій. Слово формула можна замінити словом вираз. Наприклад, виразами являються такі записи: , , , , .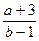

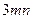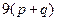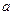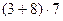Значенням виразу називається число, яке утримується, якщо в цей вираз підставити замість букв задані їх числові значення і виконати над числами вказані дії. Наприклад, вираз 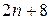при 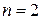дорівнює 12.

Значення виразу змінюється в залежності від зміни значень букв, які він містить.

Два вирази, з‘єднані знаком «=», утворюють рівність. Нерівністю називають вирази зі знаком >,<. Знак нерівності завжди звернений гостриком до меншого числа..

Значення, які можуть приймати букви в заданому виразі, називають допустимими значеннями для цих букв. Якщо вираз отримали в результаті розв‘язання задачі, то область допустимих значень визначається за змістом самої задачі. Якщо про вираз нічого не сказано, то для нього допустимими вважають всі ті значення букв, при яких вираз має сенс.

Порядок виконання дій.

Додавання і віднімання – дії першої ступені.

Множення і ділення – дії другої ступені (старшої).

Правила про порядок виконання дій:

1. дії однієї ступені відбуваються в тому порядку, в якому вони записані. Наприклад, 17-11+8=6+8=14, 8:2*3=4*3=12.

2. якщо вираз містить дії різних ступіней, то спочатку виконуються дії вищого ступеня, потім – нижнього. Наприклад, 3+5*7=3+35=35

3. якщо потрібно виконати раніше дії нижньої ступені, то застосовують дужки. Дії над числами, що знаходяться в дужках, виконуються раніше. Наприклад, 11-2*4=11-8=3, або (11-2)*4=9*4=36.

Якщо задано дробовий вираз, записаний за допомогою риски, то риска замінює дужки і означає, що потрібно обчислити окремо вираз, який стоїть в чисельнику, і окремо вираз, який стоїть в знаменнику, а потім перший результат поділити на другий. .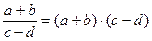

Алгебраїчні вирази, які складаються з чисел, позначених цифрами і буквами і з‘єднаних за допомогою дій додавання, віднімання, множення, ділення і підведення до степеня, називають раціональними. Наприклад, 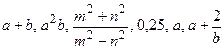. Вираз, який не містить дій ділення на вираз, називається цілим.

Одночлен

Алгебраїчний вираз, який містить лише дії множення і підведення до степеня, називають одночленом. Наприклад, 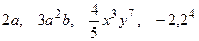.таким чином, одночлен представляє собою добуток числового множника і букв, кожна з яких взята в певній степені. Вираз, що складається з однієї лише букви, вважається одночленом, а також будь-яке число окреме являється одночленом.

Багаточлен

Алгебраїчна сума декількох одночленів називається багаточлен. Кожний одночлен називають тоді членом, 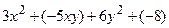. Часто багаточлен називають поліномом. За кількістю членів поліноми бувають двочленами 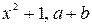, трьохчленами .

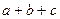Дата добавления: 2014-01-11