
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка статистических гипотез. Статистической гипотезой называется утверждение относительно параметров генеральной совокупности, сформулированное по определенным правилам
|
|
|
|
Статистической гипотезой называется утверждение относительно параметров генеральной совокупности, сформулированное по определенным правилам. Любая содержательная гипотеза может быть сформулирована в виде статистической.
Статистическая гипотеза состоит из двух утверждений. Первое утверждение, постулирующее отсутствие различий между частями ГС или связи между переменными, называется нулевой гипотезой и обозначается  . Во втором утверждении, которое называется альтернативной гипотезой и обозначается
. Во втором утверждении, которое называется альтернативной гипотезой и обозначается 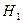 , формулируется наличие определенных различий между структурными частями ГС или связи между переменными.
, формулируется наличие определенных различий между структурными частями ГС или связи между переменными.
Статистическая гипотеза формулируется в терминах параметров ГС с использованием отношений равенства ( ) и неравенства – не равно, больше, меньше (
) и неравенства – не равно, больше, меньше (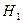 ).
).
В общем виде мы имеет две гипотезы для рассмотрения: нулевая H0 и альтернативная H1. Альтернативная гипотеза может быть односторонней (тогда как нулевая гипотеза утверждает равенство «=», одностороння альтернативная гипотеза его отрицает «≠») и двухсторонней (тут уже два вида: правосторонняя «>» и левосторонняя «<»).
Альтернативные гипотезы, в соответствии с используемым отношением неравенства, делят на двусторонние (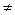 ) и односторонние (<, >); односторонние альтернативные гипотезы, в свою очередь, можно разделить на левосторонние (<) и правосторонние (>).
) и односторонние (<, >); односторонние альтернативные гипотезы, в свою очередь, можно разделить на левосторонние (<) и правосторонние (>).
Проверка статистической гипотезы состоит в том, чтобы по данным выборочного исследования сделать вывод, следует ли в отношении ГС принять нулевую гипотезу или отклонить ее в пользу альтернативной. При этом нулевая гипотеза считается справедливой до тех пор, пока не будет найдено убедительное подтверждение того, что она не верна.
Решение о принятии или отклонении нулевой гипотезы принимается в соответствии с критерием, который строится на основе специально подобранной для каждой нулевой гипотезы численной функции 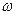 . Функция
. Функция 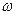 вычисляется по выборке и называется статистикой критерия.
вычисляется по выборке и называется статистикой критерия.
Поскольку решение (принять или отклонить  ) принимается на основе выборки, оно может быть как правильным, так и ошибочным. При этом возможны два типа ошибок. Ошибка, заключающаяся в том, чтобы по данным выборки отклонить нулевую гипотезу, которая на самом деле верна, называется ошибкой первого рода; ее вероятность обозначается буквой
) принимается на основе выборки, оно может быть как правильным, так и ошибочным. При этом возможны два типа ошибок. Ошибка, заключающаяся в том, чтобы по данным выборки отклонить нулевую гипотезу, которая на самом деле верна, называется ошибкой первого рода; ее вероятность обозначается буквой 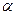 . Ошибка, состоящая в том, чтобы принять нулевую гипотезу, которая на самом деле не верна, называется ошибкой второго рода; ее вероятность обозначается буквой
. Ошибка, состоящая в том, чтобы принять нулевую гипотезу, которая на самом деле не верна, называется ошибкой второго рода; ее вероятность обозначается буквой 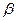 .
.
Ошибкой выборки называется разносить между значениями выборочной статистики и параметра ГС: 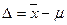 (для дихотомической переменной
(для дихотомической переменной 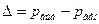 ).
).
| Ошибка выборки измеряется в тех же единицах, что и переменная. |
Если точное значение параметра неизвестно, то нельзя вычислить и точное значение ошибки выборки. В этом случае ее необходимо оценить статистически с помощью доверительного интервала.
Доверительным интервалом для ошибки выборки называется интервал, в который она попадает с заданной доверительной вероятностью  .
.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 484; Нарушение авторских прав?; Мы поможем в написании вашей работы!