Минимальный объем случайной репрезентативной выборки

Цель следующих вычислений – найти оптимальный (минимальный) объем выборки, при котором её (выборку) можно считать репрезентативной. То есть такой объем, при котором результаты исследования по выборке можно переносить на генеральную совокупность.

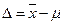
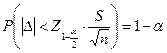
Заранее выбрав ошибку выборки (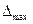), доверительную вероятность, доверительный интервал, мы можем определить, при каком объеме выборки (n) мы можем получить ожидаемый результат.

(далее мы будем называть 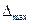допустимой ошибкой выборки - ).

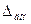Из вышеприведенной формулы нетрудно выразить объем выборки:

Формула 1.

До исследования нам неизвестна величина дисперсии (остальные неизвестные параметры, как допустимая ошибка 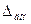и вероятность ошибки α, определяются гипотетически), и есть два способа оценить неизвестную дисперсию:

1. Провести пилотажное исследование.

2. использовать метод оценки максимальной дисперсии.

Второй метод особенно хорош в применении к дихотомическим переменным, потому как максимальная дисперсия всегда равна для дихотомических переменных 0,5 (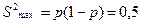). Для количественных же переменных применяется следующая формула:

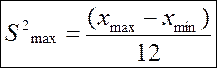(применяя в расчетах объема выборки значение максимальной дисперсии, полученное по данной выборке, в итоге можно сократить полученное значение n на 20%).

Если объем выборки (n) сопоставим с объемом генеральной совокупности (N) (составляет 20 и более процентов от N), то для определения ошибки выборки используется поправка на объем генеральной совокупности.

Если нам известен объем генеральной совокупности и генеральная совокупность не бесконечна (N≤100.000), то значение выборки, полученное по формуле 1, можно сократить за счет поправки на генеральную совокупность:

Формула 2.

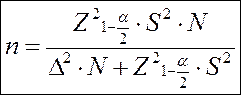
Когда же мы имеем дело с дихотомическими переменными, целесообразно применять следующую формулу:

Формула 3.

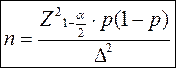
Дата добавления: 2014-01-11