Коэффициент сопряженности (контингенции) Пирсона» (C)

Применяется для квадратных таблиц, больших, чем 2х2, в которых хотя бы одна переменная не является количественно или порядковой.

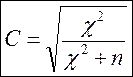
Коэффициент наиболее эффективен в случаях, когда есть чисто номинальные переменные.

3) «Коэффициент Крамера» (V):

Применяется для неквадратных таблиц.

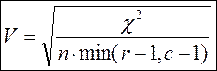(в знаменателе выбираем наименьшее число из числа строк и числа столбцов, отнимаем 1 и умножаем его на объем выборки, например, r=3, с=4 => в знаменателе: )

Все три вышеперечисленные коэффициента основаны на и имеют ряд ограничений: поскольку они могут принимать только положительный значения, они применяются для измерения только ненаправленной связи => их нельзя использовать для таблиц с обеими дихотомическими, с обеими количественными или порядковыми переменными.

Коэффициенты для измерения направленной связи:

Для следующих коэффициентов существуют собственные обозначения частот в таблице сопряженности:

y	x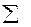
«0»	«1»
«0»	a	b	a+b
«1»	c	d	c+d
	a+c	b+d	a+b+c+d

4) «Коэффициент фи» ():

Применяется для таблиц 2х2, образованных дихотомическими переменными, при условии, что маргинальные частоты по строкам и по столбцам приблизительно равны.

Коэффициент отличается от только областью определения (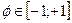), т.е. только знаком (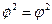). Исходя из этого можно утверждать, что

При изучении связей между переменными обязательно решаются две задачи:

1. Проверка гипотеза о наличии связи (о статистической значимости связи, т.е. возможности перенесения на генеральную совокупность).

2. Измерение силы (при необходимости направленности) связи.

В случае, когда применяется критерий последовательность можно нарушить для упрощения решения задачи.

5) «Коэффициент Юла» (Q):

Применяется для таблиц 2х2, образованных дихотомическими переменными, при условии, что маргинальные частоты по строкам и по столбцам не равны.

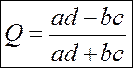
· Принимает значение +1, если b или c равны 0.

· Принимает значение -1, если a или в раны 0.

Для изучения следующих коэффициентов необходимо определить такие понятия как инверсия, совпадение и связанность переменных в таблице сопряженности:

Отношения между объектами А и В называются совпадением (С), если для переменных x и y выполняется одно из двух следующих условий:

Считается число совпадений путем умножения частоты в конкретной ячейке на сумму частот в ячейках ниже и правее данной ячейки. Затем результаты таких операций складываются.

Отношение инверсии (D) означает выполнение одного из следующих условий:

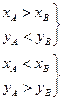
Считается число инверсий путем умножения частоты в конкретной ячейке на сумму частот в ячейках ниже и левее данной ячейки. Затем результаты таких операций складываются.

Отношение связанности по переменной x(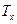) означает выполнение условия:

Считается число связанных переменных по х путем умножения частоты в конкретной ячейке на сумму частот в ячейках правее данной ячейки по той же строке. Затем результаты таких операций складываются.

Отношение связанности по переменной y () означает выполнение условия:

Считается число связанных переменных по y путем умножения частоты в конкретной ячейке на сумму частот в ячейках ниже данной ячейки по тому же столбцу. Затем результаты таких операций складываются.

Меры связи для таблиц сопряженности, образованных порядковыми (сгруппированными в интервалы количественными) переменными.

6) «Гамма Гудманна и Красколла» ():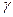

Применяется для измерения связей в таблицах с порядковыми и сгруппированными в интервалы количественными переменными.

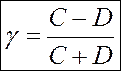
Коэффициент хорошо измеряет сильные связи и связи средней силы, однако может принимать значение 0, если существует слабая связь между переменными.

Когда связь относительно слабая и коэффициент 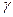приблизительно равен нулю, целесообразно применять два следующих коэффициента для оценки силы связи.

Дата добавления: 2014-01-11