
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
См. (И5) лекции №13
|
|
|
|
Пусть пл-сть колеб. совпадает с пл-ю рисунка.
Маятник имеет скорость 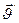 ,
,  -начальная к траектории
-начальная к траектории
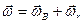 пояснения (И6)
пояснения (И6)

 ;
;
1)  -это состав. действ. вдоль нити, растягивающая ее.
-это состав. действ. вдоль нити, растягивающая ее.
2) -сила мала и она оказывает малое влияние, т. к.
-сила мала и она оказывает малое влияние, т. к.  .
.
3) 
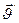 и
и 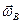 находятся в пл-ти доски. Эта сила
находятся в пл-ти доски. Эта сила  направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.
направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.

№28.Углы Эйлера.
Углы Эйлера -3 угла, которые описывают вращение системы S с тт. относительно S1.
См. (рис.1) в лекции №14.
Рис.1:  -прямая по которой пересекаются плоскости
-прямая по которой пересекаются плоскости  и
и  .
.
Дадим ряд определений:
Пл-ть 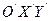 пересекает пл-ть OXY по линии
пересекает пл-ть OXY по линии  (линия узлов), полож. направление совпадает с вектором
(линия узлов), полож. направление совпадает с вектором  .
.  .
.
По определению углы Эйлера называются углы: 
Угол  является углом собственного вращения.
является углом собственного вращения.
Угол  называется углом процессии.
называется углом процессии.
Угол  называется углом нутации.
называется углом нутации.
№29.Вращательное движение.
Вращательное движение, при котором 2 его точки остаются всегда неподвижными, прямая проходящая через эти точки - называется осью вращения.
Все остальные точки не лежащие на оси описывают окружности в плоскостях оси вращения, центры этих окружностей лежат на оси вращения.
См. (И2») в лекции №14.
Рассмотрим какую либо точку, которая движ. по окружности. R-радиус, 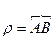 .
.

 ;
;  -угловая скорость вращения тт.
-угловая скорость вращения тт.
 см. (И3)
см. (И3)
№30.Уровнение движения твердого тела.
Мы говорили о том, что тт. есть СМТ мы доказали, что эта система обладает 6 степенями свободы, поэтому для описания СМТ необходимо 6 скалярных уравнений; 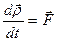 ;
; 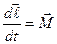 ;
;
Эти уравнения есть уравнения описывающие динамику тт. – это 6 скаляр. уравнений
Уравнения моментов можно брать относительно произвольного неподвижного начала или относительно центра масс тт.. Можно также брать произвольно движ. начало, если только скорость его в любой момент времени параллельна скорости центра масс. При ограничение свободы движ. число независимых уравнений, требующихся для описания движ. тт., уменьшается. Она всегда равна числу степеней свободы.
Внутренние силы не влияют на движ. тт.
 №31.Моменты инерции.
№31.Моменты инерции.
 (см. и5 лекции 14)
(см. и5 лекции 14)

 (1)
(1)

 (2)
(2)
(см и1 лекции15)
 (3)
(3)
представим, что 
 ,
,  (4)
(4)
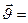 (2; 2) (см. и2)
(2; 2) (см. и2)
( не такая экзотика для полупроводников )
вывод: если между проекциями физ. Величин сущ-ет связь типа (4), причем 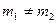 , то видим, что векторы, для которых эта связь справедлива, непараллельны
, то видим, что векторы, для которых эта связь справедлива, непараллельны

 (5)
(5)
Формула (5) уже дает связь между  и
и 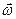 , но она достаточно неявна.
, но она достаточно неявна.
Преобразуем (5), для этого рассмотрим проекции  на оси координат.
на оси координат. ,
, 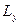

1)
 (
( ;
; ;
; )
)
(6)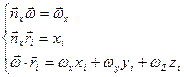

 (7)
(7)
 (8)
(8)
Формула (8) дает связь проекции  момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости
момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости 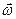
Аналогично получим:
 (9)
(9)
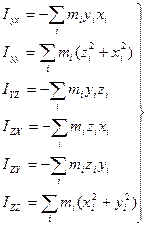 (10) Из формул (10) видно:
(10) Из формул (10) видно: 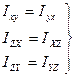 (11)
(11)
Из 9-ти коэффициентов независимы только 6.
Величины  ,
,  ,
,  называются осевыми моментами инерции тв. тела.
называются осевыми моментами инерции тв. тела.
Величины 
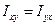 ,
, 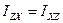 ,
,  называются центробежными моментами инерции ТТ.
называются центробежными моментами инерции ТТ.
Векторы 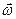 и
и 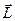 не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга.
не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга.
 (12)
(12)
Тензор  , введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.
, введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.
Величины  ,
,  и т.д., называются компонентами тензора.
и т.д., называются компонентами тензора.
Тензор  называется симметричным тензором.
называется симметричным тензором.
№32.Вычисление моментов инерции относительно оси.
(см и1 лекции 16)
Пусть ось Z есть ось вращения.
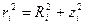
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Момент инерции относительно оси.
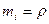 (
( ;
;  ;
;  )
)
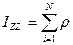 (
( ;
;  ;
; )
)




Этот предел если существует, то равен объемному интегралу
(см. и2 лекции 16)
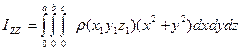 (5)
(5)
Формула (5) дает выражение для момента инерции относительно оси в случае непрерывного
расположения массы вещества.
 №33.Теорема Гюйгенса-Штейнера
№33.Теорема Гюйгенса-Штейнера
(см. рис в лекции №17)
Расм. произвольное тв. тело. Пусть точка О –центр масс этого тела, а ось 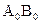 проходит через центр масс. Пусть АВ – ось //
проходит через центр масс. Пусть АВ – ось // 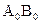 и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.
и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.
Ri отсчитывается от центра масс. 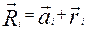 (1)
(1)
Задача: сравнить осевой момент инерции относительно оси 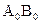 и оси АВ
и оси АВ

 от
от 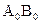
 Iо
Iо

 от АВ
от АВ I
I
 (2)
(2)
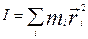 (3)
(3)
 (4)
(4)
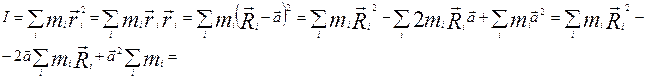
 (6)
(6)  (5)
(5)
Ф-ла (2) и (5) 

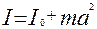 (7)
(7)
Формула (7) выражает теорему Гюйгенса-Штейнера.
№36. Движение тел с переменной массой.
 ,
,
 км/с
км/с
речь не идет о релятивистском изменении массы.
Мы называем тело телом с переменной массой если в процессе его движения масса тела меняется за счет потери или приобретения вещества.пример: 3-х ступенчатая ракета. Выгорает топливо, масса уменьшается.
Для получения уравнения движения тела с переменной массой нет необходимости привлечения новых физ. Принципов. Это ур-е следует из законов Ньютона .(см. и1 лекции 20)
Пусть имеется ракета (см и1) которая имеет массу М(t). Пусть в неподвижной ИСО S скорость ракеты равна  .Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u. Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.
.Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u. Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.
dM<0 (2) следовательно мы имеем: dM+dm=0 (3)- закон сохранения массы. Импульс системы в момент времени t:  (4)
(4)
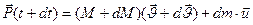 (5)
(5)
Для общего случая:  (6)
(6)
Когда действует внешняя сила: (7)
(7)
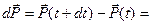

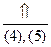 Получаем:
Получаем: 
Мы пренебрегаем произведением 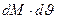 как величину 2-го порядка малости
как величину 2-го порядка малости
 (8)
(8)
Мы учтем силу для общего случая: 
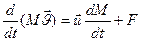 (9)
(9)
Уравнение (9) описывает движение тела с переменной массой в ИСО S при наличии внешних сил F.
 - относительная скорость газов относительно ракеты, тогда относительно S
- относительная скорость газов относительно ракеты, тогда относительно S
 (10)
(10)
 (11)
(11)
Расписываем левую часть (9):

 (12)
(12)
Обозначим через  ежесекундный расход топлива
ежесекундный расход топлива
 (13) {кг/с}
(13) {кг/с}
с учетом (3) перепишем (13)
 (14)
(14)
 (15)
(15)
Формула (15) есть главная формула данного вопроса.
Вектор  (16) назовем реактивной силой.
(16) назовем реактивной силой.
Уравнение (15) называется уравнением Мещерского или уравнением движения тела с переменной массой для общего случая(в присутствии F).
№37. Формула Циолковского.
(см. и2 в лекции 20)
 (1)
(1)
Спроецируем  с учетом (1) на ось Z
с учетом (1) на ось Z

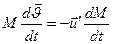
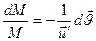 (2)
(2)
Обозначим  ,
, - значения массы и скорости перед включением двигателя ракеты
- значения массы и скорости перед включением двигателя ракеты
 const
const

 (3)
(3)
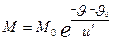 (4)
(4)
Формула (4) называется формулой Циолковского. Эта формула показывает насколько изменится масса ракеты при увеличении скорости от 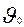 до
до  . Из этой формулы можно узнать насколько изменится скорость ракеты.
. Из этой формулы можно узнать насколько изменится скорость ракеты.  (5)
(5)
Из этой формулы видно, что для увеличения скорости при минимальном расходе топлива нужно увеличивать  .
.
 =(4~5)км/с
=(4~5)км/с
На практике используют ступенчатый принцип. Идею 3-х ступенчатой ракеты предложил Циолковский.
№38. Столкновения. Законы сохранения при столкновениях.
Пример: столкновение 2-х бильярдных шаров
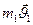

.Если шары столкнулись, скорости их изменились, при этом происходит удар. Более сложный- опыт Резерфорда в котором изучалось столкновение 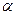 - частиц с ядрами вещества.(см. и3 лекции 20)
- частиц с ядрами вещества.(см. и3 лекции 20)
При этом скорость меняется от  до
до  , и прямого удара не было.
, и прямого удара не было.
Таким образом, есть только изменение скорости, но в физике это тоже относится к столкновению.
Столкновением называется взаимодействие 2-х или более тел (частиц) которое происходит в относительно малой области пространства и в течении малого времени, при этом скорости тел до взаимодействия и после взаимодействия измеренные в точках  и времени
и времени  отличаются друг от друга.
отличаются друг от друга.
( ) L ~ x
) L ~ x
( ) T ~ t
) T ~ t
L и T к А правило параметры установки.
При столкновениях, как правило происходит изменение импульса, момента импульса, и энергии частиц.
Выполняются законы сохранения:
 Мы учитываем рождение и уничтожение частиц.
Мы учитываем рождение и уничтожение частиц.
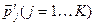
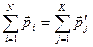 (1)
(1)
Ф - ла (1) выражает закон сохранения импульса при столкновении частиц.
Мы знаем, что при ударе часть кинетической энергии шара уходит в тепло за счет неупругих деформаций
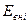 ,
,  -до удара
-до удара
 ,
,  -после удара
-после удара
 (2)
(2)
Ф – ла (2) выражает закон сохранения полной энергии при сохранении частиц.
№39. Абсолютно упругое столкновение двух шаров.
Если внутренняя энергия частиц после столкновения не изменяется, то такое столкновение называется упругим.
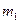 ,
, 
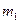 ,
,
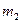 ,
,
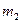 ,
,

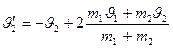
Если  , то
, то  ,
, 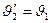 .
.
При столкновении двух одинаковых шаров, они обмениваются скоростями.
№40. Абсолютно неупругое столкновение двух шаров.
Если внутренняя энергия частиц после столкновения изменяется, то такое столкновение называется неупругим. Это столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.
Обозначим через V общую скорость шаров после столкновения. Закон сохранения импульса дает:
 , где
, где 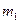 и
и 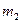 - массы шаров. Отсюда получим:
- массы шаров. Отсюда получим:
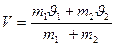
Кинетические энергии системы до удара и после удара равны соответственно:
 ,
, 
отсюда получим:
 , где
, где  - приведенная масса шаров.
- приведенная масса шаров.
Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 288; Нарушение авторских прав?; Мы поможем в написании вашей работы!