
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математический маятник
|
|
|
|
(см. Л.№17.И.6)
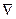 Система (И.6) и состоящая из нерастяжимой нити длиной
Система (И.6) и состоящая из нерастяжимой нити длиной 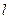 ,подвешенная в точке О. С сосредоточенной массой
,подвешенная в точке О. С сосредоточенной массой 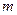 и находящаяся в поле силы тяжести называется математическим маятником.Мы считаем эту массу материальной точкой.
и находящаяся в поле силы тяжести называется математическим маятником.Мы считаем эту массу материальной точкой.
Найти закон движения м.т. на И.6 если ей сообщена либо начальная скорость, либо угол отклонения,либо начальный импульс.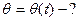
В основе решения любой задачи лежит закон природы. В данном случае это второй закон Ньютона записанный для вращательного движения 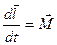 (1)
(1)
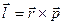 ;
; 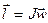 (2)
(2) 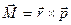 (3) Сила натяжения нити не создает момента т.к.
(3) Сила натяжения нити не создает момента т.к.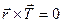 .
.
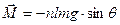 (4) Проецируем ур-е (1)
(4) Проецируем ур-е (1)  (5);
(5); 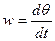 (6)
(6)
Подставляя (6) в (5) получаем: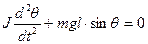 (7)
(7)
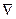 Ур-е (7) называется дифференц. Ур-ем движения математического маятника
Ур-е (7) называется дифференц. Ур-ем движения математического маятника Это не линейное ур-е.
Это не линейное ур-е.
Для решения (7) мы рассмотрим случай малых колебаний, именно он и реализуется в часах. 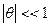 (8).
(8). 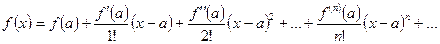 (9)
(9)
 Ф.(9) называется рядом Тейлора
Ф.(9) называется рядом Тейлора
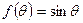 ;
; 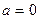 ;
; 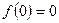 ;
; 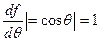
При выполнении (8) ряд Тейлора можно оборвать на первом не нулевом члене. 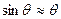 (10) С учетом (10) получаем
(10) С учетом (10) получаем  (11)
(11)
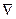 Ур-е (11) называется линейным диф. Ур-ем движения математического маятника
Ур-е (11) называется линейным диф. Ур-ем движения математического маятника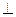
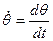 ;
; 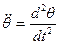 (12);
(12); 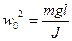 (13);
(13); 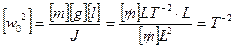
Мы показали, что этот параметр введенный по формуле (13) имеет размерность квадрат частоты. С учетом (12) и (13) и (11) приобретает следующий вид: 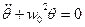 (14)
(14)
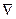 Это линейное дифференциальное ур-е движения математического маятника
Это линейное дифференциальное ур-е движения математического маятника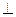
ОЗМ: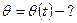
Ур-е (14) решается стандартными методами ОДУ.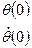 -задано (15)
-задано (15)
 В теории ОДУ ур-е (14) совместно с (15) которое записывается в след. Виде:
В теории ОДУ ур-е (14) совместно с (15) которое записывается в след. Виде: 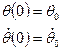 -(16) называется задачей Коши и имеет единственное решение.
-(16) называется задачей Коши и имеет единственное решение.
 Решением ур-я называется такая ф-ия
Решением ур-я называется такая ф-ия 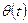 , которая будучи подставлена в ур-е (14)представляет его в верное тождество
, которая будучи подставлена в ур-е (14)представляет его в верное тождество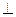
Мы покажем, что 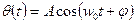 (17);
(17); 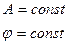 -(18) является решением.
-(18) является решением.
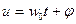 ;
; 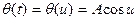 ;
;
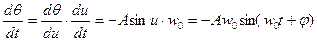 ;
;
 (19) Подставляем (19) и (17) в левую часть ур-я (14).
(19) Подставляем (19) и (17) в левую часть ур-я (14).
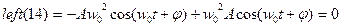
 Мы видим, что искомое решение ур-я (14) представляет собой гармоническую ф-ию времени и периодическую.
Мы видим, что искомое решение ур-я (14) представляет собой гармоническую ф-ию времени и периодическую.
 По этой причине говорят, что система изобр.на (И.6) совершает колебания, т.е.периодические движения вокруг одной точки, которая является положением равновесия.
По этой причине говорят, что система изобр.на (И.6) совершает колебания, т.е.периодические движения вокруг одной точки, которая является положением равновесия.
 Величина А в законе движения (17) называется амплитудой колебаний
Величина А в законе движения (17) называется амплитудой колебаний 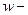 круговая частота,
круговая частота, 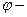 начальная фаза.
начальная фаза.
Мы показали, что 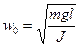 (20); из и.6 видно, что
(20); из и.6 видно, что 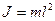 (21); (21) в (20), получим
(21); (21) в (20), получим 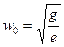 (22);
(22); 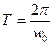 (23);
(23); 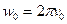 (24);
(24);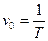 ;
; 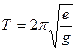 (25);
(25);
 Ф.(25) дает период колебаний математического маятника. Мы вывели ее исходя из ур-я (14) и решения (17). Отметим, что Т независит от массы, а определяется только длиной нити и ускорением
Ф.(25) дает период колебаний математического маятника. Мы вывели ее исходя из ур-я (14) и решения (17). Отметим, что Т независит от массы, а определяется только длиной нити и ускорением 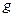 .
.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!