Определение закона распределения случайной погрешности

Задача определения закона распределения случайной погрешности решается в два этапа:

1) построение гистограммы или кумулятивной кривой распределения случайной погрешности и высказывание гипотезы о виде распределения;

2) проверка гипотезы о виде распределения с помощью критерия согласия.

Гистограмма и кумулятивная кривая являются дискретными аналогами дифференциальной и интегральной функций распределения, построенными по статистической совокупности из 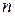результатов наблюдений. результаты наблюдений можно представить на оси в виде ранжированного ряда 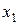, , 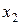…, 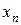. разность между наибольшим и наименьшим наблюдаемыми значениями отсчетов равна диапазону результатов наблюдения

.

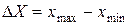Этот диапазон можно разбить на 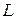интервалов длительностью

.

Число интервалов выбирают по табл. 8.1

Таблица 8.1 – Число интервалов гистограммы

	40…100	100…500	500…1000	1000…10000
	7…9	8…12	10…16	12…22

Далее определяют границы интервалов 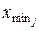и и их середины 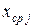по формулам

; ;

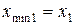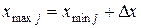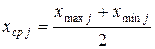
и считают, количество 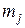результатов наблюдений, попавших в каждый 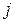–й интервал.

Строят гистограмму в виде столбиков шириной 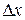и высотой .

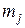Определяют вероятность того, что результаты наблюдений 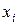окажутся меньше, чем границы интервалов

,

то есть

; ; ; …; ; .

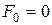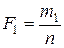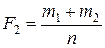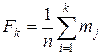Далее строят кумулятивную кривую .

После построения кумулятивной кривой и гистограммы можно высказать гипотезу о виде распределения.

Правдоподобие гипотез о соответствии распределения результатов наблюдений выбранному закону проверяют с помощью т.н. критериев согласия, одним из которых является критерий Пирсона ((1857 – 1936) английский математик, биолог, философ).

В качестве меры расхождения экспериментальных данных с теоретическим дифференциальным законом распределения вероятностей в критерии Пирсона принимается величина

,

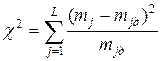где 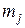– число результатов наблюдений, попавших в 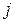-й интервал гистограммы;

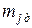– действительное число результатов наблюдений, которые попали бы в 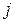-й интервал при полном соответствии эмпирического закона распределения гипотетическому.

Значение 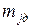рассчитывается по формуле

,

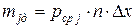где – значение гипотетической функции распределения в точке, соответствующей средине 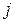-го интервала гистограммы;

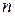– общее число наблюдений;

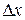– ширина интервала гистограммы.

Величина 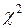распределена по закону Пирсона. Это распределение зависит от параметра 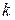, называемого числом степеней свободы.

Число степеней свободы равно числу интервалов гистограммы 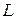минус число независимых условий, наложенных на эмпирическое распределение. Для симметричных законов распределения такими условиями являются:

1) условие нормировки ;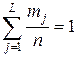

2) требование равенства математического ожидания гипотетического распределения среднему арифметическому экспериментального распределения ;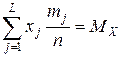

3) требование равенства дисперсии гипотетического распределения оценке дисперсии экспериментального распределения

.

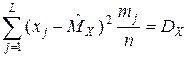Поэтому 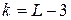. Для распределения Пирсона составлены соответствующие таблицы, пользуясь которыми можно найти для каждого числа степеней свободы и заданной вероятности 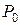величину 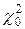. Если 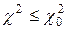, то гипотеза о виде закона распределения подтверждается, если 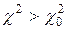– отклоняется.

При проверке закона распределения по критерию Пирсона хорошие результаты получаются только при . Для 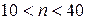применяют составной критерий.

Дата добавления: 2014-01-11