Определение точечных оценок числовых характеристик эмпирических законов распределения случайной погрешности

В отличие от самих числовых характеристик их оценки являются случайными величинами, причем их значения и рассеянность зависят от числа экспериментальных данных.

Точечные оценки числовых характеристик должны удовлетворять трем требованиям: они должны быть состоятельными, несмещенными и эффективными.

Состоятельной называется оценка, которая с увеличением выборки приближается к истинному значению характеристики

; .

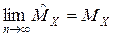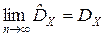По определению математического ожидания

.

Так как каждое значение 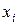появляется один раз при общем объеме выборки 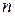, то 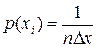, откуда

.

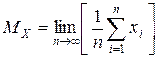При конечном 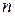оценкой 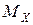является среднее арифметическое

.

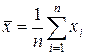Поскольку 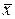появилось из 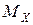при ограничении объема выборки, то 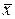является состоятельной оценкой математического ожидания.

По определению дисперсии

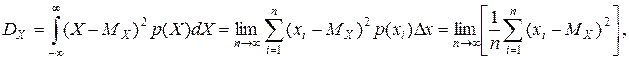то есть состоятельной оценкой 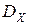является так называемая выборочная дисперсия

.

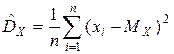На практике 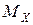неизвестно, поэтому при расчете математическое ожидание заменяют оценкой :

.

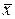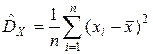Это не влияет на состоятельность оценки 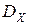, поскольку .

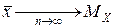Несмещенной называется оценка, математическое ожидание которой равно самой характеристике

; .

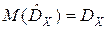Проверим несмещенность среднего арифметического

.

Таким образом, среднее арифметическое является несмещенной оценкой математического ожидания результатов многократных наблюдений при любом законе распределения.

Проверим несмещенность оценки дисперсии:

Так как

,

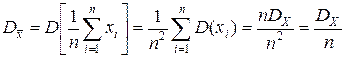то

.

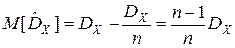Таким образом, замена математического ожидания на среднее арифметическое приводит к смещению оценки дисперсии.

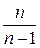Несмещенную оценку получают путем домножения на коэффициент , то есть несмещенной оценкой дисперсии является

.

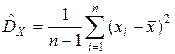При 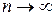коэффициент 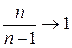, поэтому эта оценка является также состоятельной.

Оценка СКО результата наблюдения определяется, как правило, по формуле

.

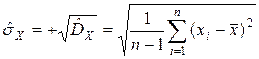Эффективной называется оценка, обладающая наименьшей дисперсией (рассеянием) по сравнению с остальными.

Для выбора наиболее эффективной оценки существует целый ряд методов. Наиболее распространенным является метод максимального правдоподобия, теоретически обоснованный сэром Рональдом Эйлмером Фишером (1890 – 1962), английским статистиком, биологом–эволюционистом и генетиком. Идея метода заключается в нахождении таких оценок параметров распределения, при которых достигает максимума т.н. функция правдоподобия. Последняя определяется как вероятность появления всех независимых результатов наблюдения 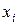. Математически эту задачу можно решить для конкретного вида дифференциальной функции распределения.

Для симметричных законов распределения эффективные оценки математического ожидания и СКО можно определить по значению эксцесса (оценки островершинности)

.

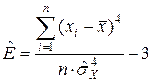Если 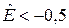, то есть распределение близко к равномерному, то наиболее целесообразно оценкой математического ожидания считать полуразмах (табл. 8.2).

Если 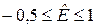, то есть распределение близко к нормальному (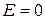), то за оценку математического ожидания лучше взять среднее арифметическое.

Если 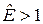, то есть распределение близко к экспоненциальному (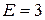), то за оценку математического ожидания лучше взять медиану.

Таблица 8.2 – эффективные оценки математического ожидания и СКО симметричных распределений

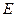
	<–0,5	–0,5…1	>1

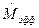
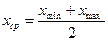
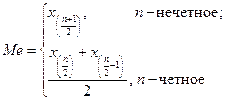
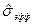
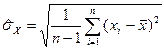
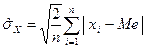
Дата добавления: 2014-01-11