
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Суммирование погрешностей
|
|
|
|
Погрешность измерения, как правило, вызывается разнообразными одновременно действующими причинами и поэтому может состоять из большого числа 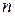 составляющих. Рассмотрим, как из этих составляющих
составляющих. Рассмотрим, как из этих составляющих 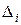 , считаемых независимыми, формируется результирующая погрешность
, считаемых независимыми, формируется результирующая погрешность
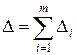 .
.
Каждую из составляющих 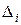 можно рассматривать как случайную величину, имеющую свой закон распределения. Очевидно, что закон распределения
можно рассматривать как случайную величину, имеющую свой закон распределения. Очевидно, что закон распределения 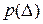 результирующей погрешности
результирующей погрешности 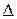 является композицией распределений
является композицией распределений 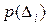 составляющих
составляющих 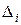 . При этом математическое ожидание
. При этом математическое ожидание 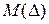 и дисперсия
и дисперсия 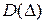 распределения результирующей погрешности являются суммами соответственно математических ожиданий и дисперсий составляющих
распределения результирующей погрешности являются суммами соответственно математических ожиданий и дисперсий составляющих 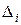 :
:
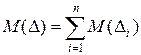 ;
; 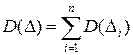 .
.
Известно, что каждая из составляющих включает в себя две компоненты – случайную 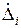 и систематическую
и систематическую 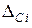 . Из вероятностного представления погрешности следует, что поскольку
. Из вероятностного представления погрешности следует, что поскольку  и
и 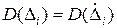 , то
, то
 ;
;  .
.
Таким образом, при формировании результирующей погрешности 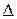 систематические составляющие суммируются арифметически.
систематические составляющие суммируются арифметически.
Случайные погрешности характеризуются своими границами 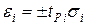 . Границы случайной компоненты результирующей погрешности будут равны
. Границы случайной компоненты результирующей погрешности будут равны
 .
.
Если известны не СКО случайных погрешностей, а их границы, то
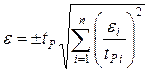 .
.
Таким образом, границы суммарной погрешности 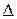 будут определяться выражением
будут определяться выражением
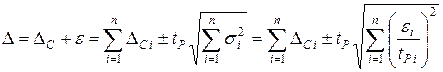 .
.
Значение доверительного коэффициента 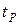 зависит от доверительной вероятности
зависит от доверительной вероятности 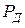 и вида суммарного распределения случайных составляющих погрешности
и вида суммарного распределения случайных составляющих погрешности 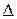 , который зависит от числа случайных составляющих
, который зависит от числа случайных составляющих 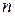 и законов их распределения.
и законов их распределения.
Таблица 8.5 – Значения доверительного коэффициента 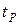 для доверительной вероятности
для доверительной вероятности 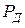 и вида суммарного распределения случайных составляющих погрешности
и вида суммарного распределения случайных составляющих погрешности 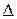
| Законы распределения | 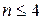
| 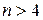
|
| Известны | 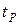 для композиции законов распределения для композиции законов распределения
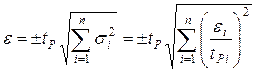
| 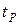 для нормального закона для нормального закона
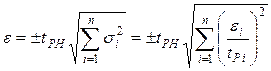
|
| Нормальные | 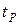 для нормального закона для нормального закона
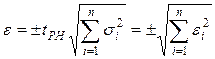
| |
| Неизвестны (считаются равномерными) | 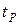 для композиции равномерных законов распределения для композиции равномерных законов распределения
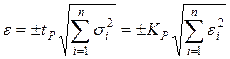
| 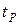 для нормального закона для нормального закона

|
Для 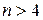 независимо от законов распределения
независимо от законов распределения 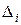 , их композиция близка к нормальному закону, поэтому
, их композиция близка к нормальному закону, поэтому 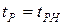 . Композиция нормальных законов распределения для любого
. Композиция нормальных законов распределения для любого 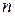 также является нормальным распределением, поэтому
также является нормальным распределением, поэтому
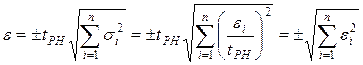 .
.
При неизвестном законе распределения 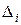 считают, что любое значение погрешности на доверительном интервале
считают, что любое значение погрешности на доверительном интервале 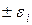 равновероятно, поэтому закон распределения всех
равновероятно, поэтому закон распределения всех 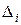 принимается равномерным. Для равномерного закона
принимается равномерным. Для равномерного закона 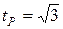 для
для 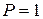 , поэтому для
, поэтому для 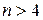
 .
.
При 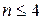 доверительный коэффициент
доверительный коэффициент 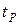 определяется для композиции
определяется для композиции 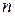 равновероятных законов распределения, для которой при равных
равновероятных законов распределения, для которой при равных 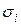
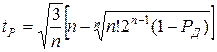 .
.
При 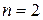 композиция дает треугольное распределение, при
композиция дает треугольное распределение, при 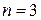 – параболическое распределение и т.д.
– параболическое распределение и т.д.
Таблица 8.6 – Значения коэффициентов 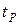 для композиции равномерных законов
для композиции равномерных законов
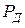
| 0,9 | 0,95 | 0,99 | 0,9973 |
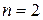
| 1,675 | 1,901 | 2,204 | 2,332 |
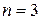
| 1,661 | 1,937 | 2,379 | 2,598 |
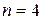
| 1,658 | 1,94 | 2,445 | 2,73 |
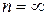 (нормальный)
(нормальный)
| 1,64 | 1,96 | 2,58 |
Если неизвестные законы распределения заданы границами 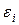 , то при
, то при 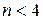
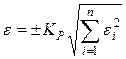 ,
,
где зависимость коэффициента 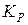 от числа слагаемых
от числа слагаемых 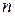 и соотношения между погрешностями
и соотношения между погрешностями 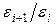 табулировано.
табулировано.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 396; Нарушение авторских прав?; Мы поможем в написании вашей работы!