Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

Перевод чисел из шестнадцатеричной системы в десятичную

Перевод чисел из восьмеричной системы в десятичную

Возьмем любое восьмеричное число, например 67,5₈.

Запишем его в развернутой форме и произведем вычисления:

67, 5₈= 6·8¹ + 7·8°+ 5·8^-1 = 6·8 + 7·1 + 5·1/8 = 55,625₁₀.

Возьмем любое шестнадцатеричное число, например 19F₁₆.

Запишем его в развернутой форме (при этом необходимо помнить, что шестнадцатеричная цифра F соответствует десятичному числу 15) и произведем вычисления:

19F₁₆ =1·16² + 9·16¹ + F·8⁰ = 1·256 + 9·16 +15·1=????

Перевод чисел из десятичной системы в двоичную, восьме­ричную и шестнадцатеричную более сложен и может осуще­ствляться различными способами. Рассмотрим один из алго­ритмов перевода на примере перевода чисел из десятичной системы в двоичную.

При этом необходимо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут различаться.

Алгоритм перевода целых десятичных чисел в двоичную систему счисления.

Пусть А — целое десятичное число. Запишем его в виде суммы степеней основания 2 с двоичными коэффициентами.

В его записи в развернутой форме будут отсутствовать отрицательные степени основания (числа 2):

A₁₀ =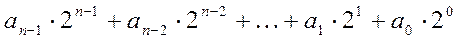

На первом шаге разделим число А на основание двоичной системы, то есть на 2.

Частное от деления будет равно

а остаток — равен a₀.

На втором шаге целое частное опять разделим на 2, остаток от деления будет теперь равен а_1.

Если продолжать этот процесс деления, то после n-го шага получим последовательность остатков:

Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме:

А₂ =

Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число.

Алгоритм перевода целого десятичного числа в двоичное будет следующим:

1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на осно­вание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.

2. Записать полученные остатки в обратной последовательности.

Дата добавления: 2014-01-11