Особенности формирования потоков

Способы задания потоков вызовов.

ТЕМА 1. ПОТОКИ ВЫЗОВОВ.

Под потоком вызовов понимается последовательность вызовов, поступающих через какие-либо промежутки или в какие-либо моменты времени.

Поток вызовов можно представить:

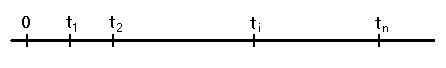
Рис. 1.1 – К определению потоков вызовов.

Здесь:

t1-момент поступления 1-го вызова;

ti-момент поступления i-го вызова;

Отсюда наглядно видно, что поток вызовов можно задать моментами времени

t1, t2, t3, …, ti, …, tn.

Под моментами времени ti понимают конец отрезка времени [0, ti), где 0 –включен в отрезок, ti – не включен в отрезок.

Потоки вызовов можно задать:

Ø Последовательностью моментов времени, когда поступают вызовы.

Ø Последовательностью промежутков между вызовами.

Ø Последовательностью чисел, определяющих количество вызовов в течение отрезка времени:

[0, t1), [0, t2), …

Различают потоки детерминированные и случайные.

Потоки, в которых вызовы поступают в строго фиксированные моменты времени, называются детерминированными.

Потоки, в которых вызовы поступают в случайные моменты времени, называются недетерминированными или случайными.

Рассмотрим потоки, в которых в любой момент времени может поступить не более одного вызова.

Такие потоки могут задаваться:

1. Последовательностью моментов поступления вызовов.

Рис. 1.2 – Первый способ задания потоков вызовов.

Поток вызовов задается последовательностью чисел t1, t2, t3, …, ti, tj … где: ti, tj – моменты поступления вызовов, при этом tj > ti, если j > i.

tj - конец отрезка [0, tj),

ti - конец отрезка [0, ti).

2. Поток вызовов задается последовательностью промежутков между вызовами

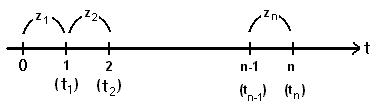
Рис. 1.3 – Второй способ задания детерминированных потоков.

0 – начало отсчета

(z1 ¹ z2) …………(zn-1 ¹ zn) …

Поток вызовов задается последовательностью чисел z1, z2, z3, … zn.

Z1 – промежуток между началом отсчета и t1 (момент поступления первого вызова).

Легко видеть, что знание последовательности чисел t1, t2, t3, …, tn позволяет определить последовательность

z1, z2, z3, … zn

z1 =t1, т.к. t1 =[0, t1),

z2 =t2- t1

…

zn =tn- tn-1.

И наоборот, зная последовательности чисел z1, z2, z3, … zn, можно найти последовательности чисел t1, t2, t3, …, tn

t1=z1

t2= z1+z2

…

tn= z1+z2 + … + zn

Таким образом, оба рассмотренные задания потоков являются эквивалентными.

3. Поток вызовов задается последовательностью чисел, представляющих собой количество вызовов, поступивших в течение отрезка времени.

Введем функцию x(t) – число вызовов, поступивших от начала отсчета до момента времени t.

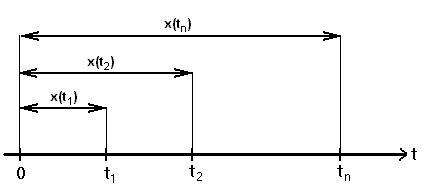
[0, t1) ® x(t1),

[0, t2) ® x(t2),

…

[0, tn) ® x(tn).

Построим функцию x(t)=f(t):

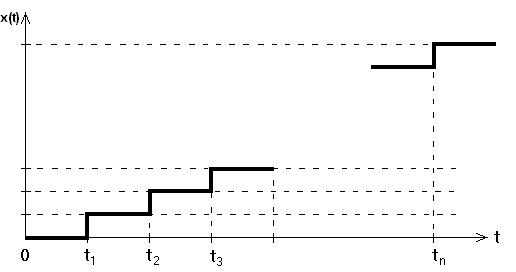Рис. 1.5 – Зависимость x(t) = f(t).

В любой момент времени поступает не более одного вызова. Как видно из графика x(t) = f(t), эта функция является неубывающей ступенчатой, претерпевающей скачки, равные 1 в каждый момент поступления вызова.

Если известна x(t), то можно определить последовательность моментов поступления вызовов, т.е.

t1, t2, t3, …, tn.

Зная последовательность t1, t2, t3, …, tn можно, как было показано ранее, перейти к последовательности z1, z2, z3, … zn, т.е. все три способа задания потоков являются эквивалентными.

На практике обычно имеют место не детерминированные потоки, а случайные. В случайных потоках вызовы поступают через случайные промежутки времени и в случайные моменты времени.

Однако задать случайный поток можно также с помощью трех рассмотренных способов, но в вероятностном смысле:

Ø Моменты поступления вызовов;

Ø Промежутки между моментами поступления вызовов;

Ø Последовательностью чисел, характеризующих количество вызовов в промежуток времени.

1. Поток вызовов задается последовательностью моментов поступления вызовов

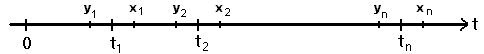Рис. 1.6 – Первый способ задания случайных потоков вызовов.

Пусть с вероятностью Р момент поступления 1-го вызова t1 ограничен отрезком времени [y1, x1), где:

y1 - [0, y1), x1 - [0, x1),

т.е. y1 £ t1 £ x1.

Момент поступления второго вызова лежит на отрезке

[y2, x2), т.е.

y2 £ t2 £ x2

………..

yn £ tn £ xn

Поток вызовов задан в вероятностном смысле последовательностью моментов поступления вызовов, если задана вероятность того, что

P{ y1 £ t1 £ x1, y2 £ t2 £ x2, …,yn £ tn £ xn },

где: y1 < y2 < … < yn;

x1 < x2 < … < xn.

Отметим еще раз, что отрезки времени y1, x1, y2, x2, …, yn, xn имеют общее начало отсчета.

2. Рассмотрим способ задания с помощью промежутков времени между соседними вызовами.

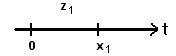Пусть с какой-то вероятностью Р промежуток z1, не будет превышать промежуток [0, x₁),

с этой же вероятностью – Р z2 < [0, x2)

и так далее, и наконец, с вероятностью Р

zn < [0, xn).

Отметим, что у промежутков [0, x1), [0, x2), …, [0, xn) имеется общее начало отсчета – 0. Тогда можно сказать, что с вероятностью Р справедливо

z1<x1, z2<x2, …, zn<xn.

Поток вызовов задается в вероятностном смысле, если известна последовательность z1, z2, z3, … zn и для любого значения n задана вероятность того, что

P{ z1 < x1, z2 < x2, …, zn < xn,},

Где отрезки x1, …, xn соответствуют соответственно отрезкам

[0, x1), [0, x2), …, [0, xn).

Запишем короче:

P{ zi < xi, },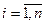

Обозначим через F(x) функцию распределения промежутков между вызовами

F(x)= P{ z < x}.

Если промежутки между вызовами взаимно независимы, то

P{ zi < xi, 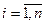} = F(x1) F(x2) … F(xn) = .

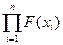3. Задание потока вызовов последовательностью чисел, определяющих количество вызовов, поступающих на заданный отрезок времени.

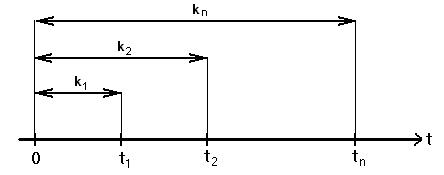Рис. 1.7 – Третий способ задания потоков вызовов.

Пусть за время [0,t1) с вероятностью Р поступит k1 вызов

x(0,t1)= x(t1) = k1

За отрезок времени [0,t2) поступит k2 вызовов

x(0,t2)= x(t2) = k2

И, наконец:

x(0,tn)= x(tn) = kn

Тогда поток вызовов задается последовательностью x(t1), x(t2), …, x(tn), если для любого n задана вероятность

P {x(t1)=k1, x(t2)=k2, …, x(tn)=kn}

Здесь t1, t2, …, tn - произвольные моменты времени и необязательно моменты поступления вызовов.

Как и прежде:

t1<t2<…<tn;

k1£k2£…£kn.

Запишем выражение для вероятности поступления k вызовов за отрезок времени в более компактном виде:

P{x(ti)=ki, }.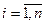

1.2 Принципы классификации потоков вызовов.

Потоки вызовов классифицируются с точки зрения стационарности, ординарности и последействия.

1. Стационарность потока.

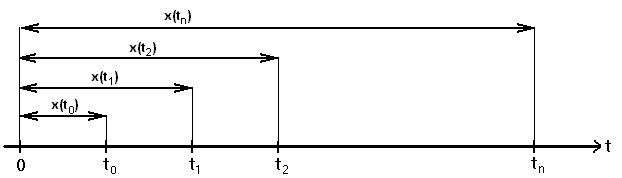Рис. 1.8 – Зависимость x(t) = f(t).

Пусть за промежуток [0,t₀) с какой-то вероятностью Р поступит x(t₀) вызовов; с той же вероятностью за промежуток [0,t₁) поступит x(t₁) вызовов и т.д.

[0,t₀) ® x(t₀) вызовов;

[0,t₁) ® x(t₁) вызовов;

[0,t₂) ® x(t₂) вызовов;

…

[0,t_n) ® x(t_n) вызовов.

Нас интересует количество вызовов, поступивших за отрезки времени

[t₀,t₁) – x(t₀,t₁) = x(t₁) – x(t₀)

[t₀,t₂) – x(t₀,t₂) = x(t₂) – x(t₀)

…

[t₀,t_n) – x(t₀,t_n) = x(t_n) – x(t₀)

Поток вызовов называется стационарным, если вероятность того, что за время [t₀,t₁) поступит x(t₀,t₁) вызовов; за время [t₀,t₂) – x(t₀,t₂) и т. д., а вероятность

P{x(t₀,t₁); x(t₀,t₂); …; x(t₀,t_n)}

зависит от промежутков времени [t₀,t₁), [t₀,t₂), …, [t₀,t_n) и не зависит от временного положения общего начала отсчета – t₀ .

Иными словами: где бы ни был на оси времени t₀, вероятность поступления

P{x(t₀,t₁), …, x(t₀,t_n)}

зависит только от отрезка времени [t₀,t_i); вероятность поступления того или иного числа вызовов зависит от длины временного промежутка и не зависит от его местоположения на оси времени.

Обозначим через 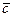- среднее число вызовов в единицу времени.

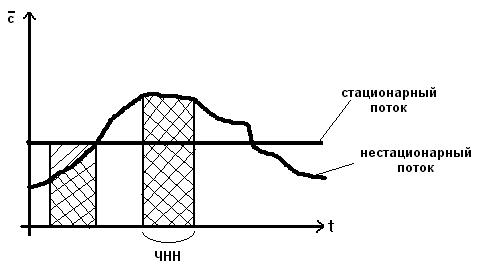Рис. 1.9 – Среднее число вызовов по часам суток.

В ЧНН считают поступающий поток стационарным.

Поток вызовов называется нестационарным, если вероятность поступления того или иного числа вызовов зависит как от длины отрезка, так и от момента его начала.

2. Последействие потока.

Поток вызовов называется потоком с последействием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала рассматриваемого промежутка времени.

ПРИМЕР: Если с аппарата вызовы не поступают, то вероятность поступления вызовов – Р₁, если вызов поступил, то во время разговора вероятность поступления вызова с этого аппарата равна нулю в данный момент времени.

Имеем загруженные телефонные аппараты: при занятости их возникает поток повторных вызовов, после ответа этот поток уменьшается.

Поток вызовов называется потоком без последействия, если вероятность поступления вызова P{x(t₀,t₁), …, x(t₀,t_i), 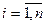} не зависит от процесса поступления вызовов до момента времени t₀.

ПРИМЕР: При большой емкости сети поток вызовов без последействия.

Поток без последействия в некоторых случаях может зависеть от момента времени t₀ (если поток нестационарный)

Если t₀ выбрать ночью, то поток один, если днем, то поток будет другим.

Принято считать, что на телефонных сетях имеют место потоки без последействия.

3. Ординарность потока.

Введем следующие обозначения:

p_k[t; t+t) – вероятность того, что за время [t; t+t) поступит k и более вызовов (k = 1,2,…).

Поток вызовов называется ординарным, если вероятность поступления 2-х и более вызовов в течение отрезка времени [t; t+t) есть бесконечно малая более высокого порядка малости, чем t при t®0 или

p₂[t; t+t) = о(t) при t®0

или

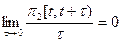
Практически ординарность потока означает, что в любой момент времени может поступить не более одного вызова.

1.3 Основные характеристики потоков вызовов.

1. Ведущая функция потока вызовов (L);

2. Интенсивность потока вызовов (m);

3. Параметр потока вызовов (l).

Математическое ожидание числа вызовов, поступающих в интервале времени [0; t), называется ведущей функцией потока.

Обозначим эту функцию L(0,t). Функция L(0,t) – неотрицательная, неубывающая и в практических задачах принимает конечное значение.

Потоки с непрерывной ведущей функцией называются регулярными, а со ступенчатой – сингулярными. В дальнейшем будут рассматриваться только регулярные потоки.

Интенсивность потока является характеристикой стационарных потоков.

Под интенсивностью стационарного потока m понимают математическое ожидание числа вызовов, поступающих в единицу времени.

За единицу времени принимают среднее время обслуживания одного вызова.

Для нестационарных потоков существуют характеристики:

а) Средняя интенсивность потока за отрезок времени [a,b) - ;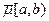

б) Мгновенная интенсивность m(t).

Рис. 1.10 – К определению интенсивности потоков.

За время [0,a) поступает L(0,a) вызовов;

За время [0,b) поступает L(0,b) вызовов.

Тогда средняя интенсивность потока за отрезок [a,b) есть:

.

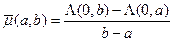L(0,а), L(0,b) – математическое ожидание числа вызовов, поступающих в течение отрезков [0,а), [0,b).

L(0,а), L(0,b), L(0,t) – ведущая функция потока.

Мгновенная интенсивность.

Рис. 1.11 – К определению мгновенной интенсивности потока вызовов.

За время [0,t) поступает L(0,t) вызовов,

За время [0,t+t) поступает L(0,t+t) вызовов.

Здесь L(0,t), L(0,t+t) – ведущие функции потока

;

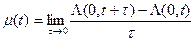Мгновенная интенсивность – это производная ведущей функции потока.

Параметр потока

Под параметром потока l в момент времени t понимается предел отношения вероятности поступления 1-го и более вызовов за отрезок времени [t, t+t] при t ®0 к этому промежутку времени при t® 0

Это плотность вероятности поступления вызовов в момент времени [t,t+t].

Для стационарных потоков l(t)=l, т.е. не зависит от момента, к которому относится параметр.

Из определения следует

p₁(t,t+t)=l(t)×t+0(t) при t®0

В последнем 0(t)- бесконечно малая более высокого порядка чем t®0

Тогда для стационарных потоков p₁(t,t+t)=lt+0(t), t®0

Какова связь между m и l? (теорема Королюка - Зитека)

Для стационарных потоков (без док-ва)

m.³l

Для стационарных ординарных потоков

m=l

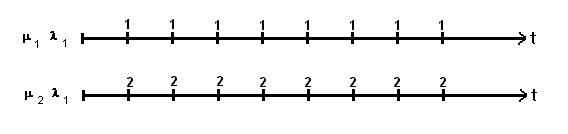
Рис.1.11 - Иллюстрация теоремы Королюка-Зитека.

Пусть на первой оси стационарный ординарный поток с m.₁ и l₁. В силу выше изложенного m₁=l_1.

На второй оси показан неординарный поток, т.к. в каждый момент поступает 2 вызова

В каждый момент времени

m₂=2m₁=2l₁

Моменты поступления вызовов зависят от l и определяются им, но l не зависит от того сколько вызовов поступит в момент времени.

1.4 Простейший поток вызовов.

На практике в качестве модели реальных потоков часто используют простейший поток вызовов.

Простейший поток вызовов - это ординарный, стационарный поток без последействия.

Математическая модель простейшего потока.

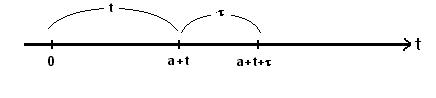Рассмотрим отрезок времени 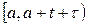и определим вероятность того, что в течение этого отрезка поступит ровно k вызовов,

т.е. Р_к(а,а+t+t).

Представим этот отрезок времени двумя

[а,а+t) и [а+t,а+t+t)

или [а,а+t+t)=[а,а+t)+[а+t,а+t+t)=[а,а+t)+[t,t+t).

Таким образом, имеем

[а,а+t+t)=[а,а+t)+[t,t+t).

За это время согласно условию должно поступить k вызовов.

Возможны следующие случаи:

За I отрезок поступит За II отрезок

1.k вызовов 0 вызовов

2. k-1 1

3. k-2 2

………………………………………………….

.…………………………………………………

………………………………………………….

k-i i

…………………………………………………..

0 k

Введем обозначения:

Р_к-i(а,а+t)- вероятность поступления k-i вызовов за отрезок времени [а,а+t),

Р_i(t,t+t)- вероятность поступления i вызовов за время [t,t+t).

Тогда искомую вероятность можно найти, как произведение вероятностей

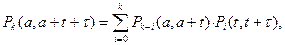
т.к. поток простейший, т.е. без последействия и, следовательно, поступление k-i вызовов и i вызовов- события независимы. Устремим t®0.

Тогда в силу ординарности потока за t®0 может поступить только 1 либо 0 вызовов. Откуда

.

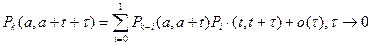Здесь 0(t) учитывает вероятность поступления 2 и более вызовов за t®0.

Вместо i поставим его значение

Р_k(а,а+t+t)=Р_k-1(а,а+t)P₁(t,t+t)+Р_k(а,а+t)×Р₀(t,t+t)+0(t) при t®0, k=0,1,2…..

Напомним, что k число за промежуток [а,а+t+t). Вероятность того, что за [t,t+t) поступит только один вызов

Р₁(t,t+t)=p₁(t,t+t)-p₂(t,t+t).

Из определения параметра потока

p₁(t,t+t)=lt+0₁(t), t®0

В силу ординарности потока

p₂(t,t+t)=0₂(t)

Перед бесконечно малыми величинами всегда ставим знак плюс, т.к. вероятность не может быть отрицательной.

Тогда

Р₁(t,t+t)=lt+0₁(t)

Р₀(t,t+t)=p₀(t,t+t)-p₁(t,t+t)=1-lt+0₂(t) при t®0.

Здесь Р₀(t,t+t)- вероятность поступления точно нуля вызовов за время [t,t+t), а вероятность поступления 0,1,2… вызова за [t,t+t]

p₀(t,t+t)=1, т.е. явл. достоверное.

Индексы 1,2….. в 0(t) указывает на различия между бесконечно малыми величинами.

Таким образом,

Р_k(а,а+t+t)=P_k-1(а,а+t)[lt+0 ₁(t)]+Р_k(а,а+t)[1-lt+0 ₂(t)]+0₃(t) при t®0 k=0,1,2…

Перенесем из правой части в левую Р_k(а,а+t) и поделим обе части на t

;

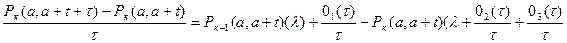t®0, k=0,1,2…¥

устремим пределу обе части уравнения

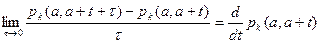, т.к.

.

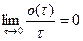Получим

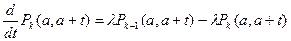при k=0,1…,¥.

Итак, имеем систему дифференциальных уравнений, которые будем решать методом производящих функций, который является основным методом комбинаторного анализа.

Идея метода заключается в следующем:

Есть последовательность

а₀,а₁,……………., а_к…

Производящей функцией этой последовательности является сумма ряда

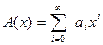
Если известно, что последняя сумма сходится в окрестности точки х=0, то ищется ряд А(х).Далее, имея ввиду однозначное соответствие между членами обоих рядов, нетрудно найти все члены первой последовательности.

В нашем случае имеем

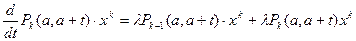при k=0,1,2…

Суммируя обе части уравнения

.

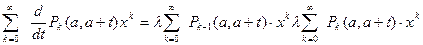Сумма производных равна производной суммы (свойства аддитивности производной).

.

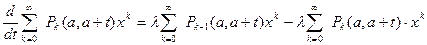обозначим

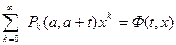- производящая функция, зависящая от t и х,

а выражение

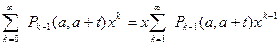
т.к. при k=0 это выражение смысла не имеет (Р_-1).

Обозначим k-1=n,

если k=1, то n=0,

если k=¥, то n=¥

Перейдя к новой переменной суммирования

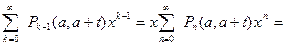
вместо n напишем снова k

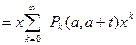
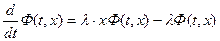
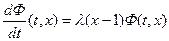
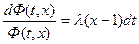
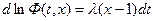
Интегрируем обе части от 0 до t

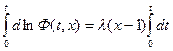
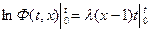
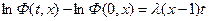
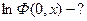
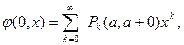т.к. t=0.

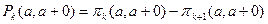
В силу ординарности потока

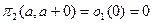
следовательно при k=2,3…

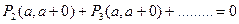
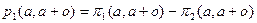
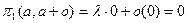
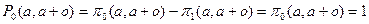
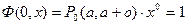
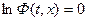
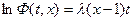
или

,

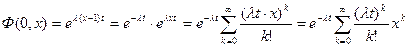т.к.

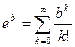
вместо Ф(t,x) подставим его значение.

В результате получаем формулу Пуассона, которая определяет вероятность того, что на интервале времени (t) поступит точно (k) вызовов.

.

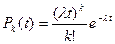Принимая t=1:

.

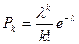Графическая иллюстрация:

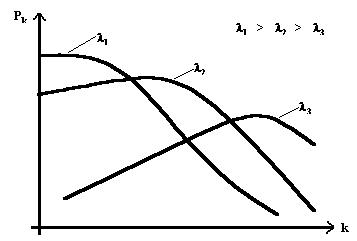Рис. 1.12 – Завмсимость P_k=f(k).

Из рисунка видно, что при увеличении l форма огибающей закона Пуассона приближается к нормальному закону распределения. При l>10 они практически сливаются.

Покажем, что формула Пуассона является законом распределения СВ (k).

.

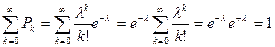Таким образом, формула Пуассона обладает основным свойством любого закона распределения.

Можно показать, что сумма независимых простейших потоков образует также простейший поток с параметром, равным сумме параметров объединяемых потоков.

Для распределения Пуассона справедливы следующие соотношения:

При t=1:

.

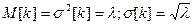1.5 Интенсивность простейшего потока вызовов.

Определим интенсивность простейшего потока:

.

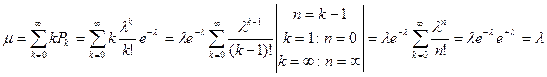Таким образом, интенсивность простейшего потока равна его параметру, что является следствием ранее сформулированной теоремы Королюка – Зитека.

Напомним ее смысл.

Для стационарных потоков справедливо неравенство m³l. Для стационарных ординарных потоков m=l, т.к. число вызовов совпадает с числом вызывающих моментов.

1.6 Функция распределения промежутков

между вызовами простейшего потока.

Согласно определению функция F(x) есть вероятность того, что промежуток между вызовами (z) окажется меньше константы (х), что равносильно вероятности p₁(х) того, что на интервале (х) поступит один и более вызовов.

.

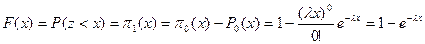Проиллюстрируем полученную зависимость графически.

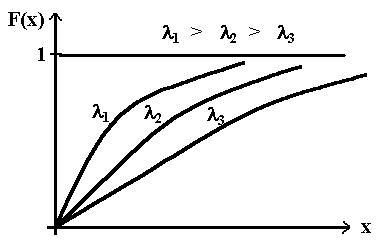Рис. 1.13 – Зависимость F(x)=f(x).

Таким образом, закон распределения СВ (z) или плотность распределения вероятностей промежутков между вызовами имеет вид:

.

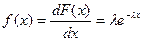Математическое ожидание и дисперсия промежутков между вызовами:

;

;

.

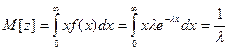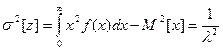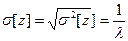Из приведенных выражений видно, что с увеличением параметра потока (l) величина промежутков между вызовами уменьшается и наоборот.

Заметим, что распределение промежутков между вызовами по показательному закону является не только необходимым, но и достаточным условием простейшего потока. Можно показать, что поток с независимыми промежутками между вызовами, распределенными по одинаковому закону, является простейшим потоком.

Показательный закон обладает следующим замечательным свойством: если промежуток времени, распределенный по показательному закону, длится некоторое время, то это никак не влияет на распределение оставшейся части промежутка: он будет таким же, как и закон распределения самого промежутка.

Показательный закон – единственный, обладающий таким свойством. Физический смысл этого свойства – отсутствие последействия. С другой стороны равенство M[z] и s[z] позволяет существенно упростить аналитические выражения, в частности, при анализе процессов поступления вызовов и их обслуживании.

1.7 Закон распределения длительности обслуживания вызовов.

В ТТ длительность обслуживания вызовов обычно принимается постоянной либо случайной величиной. Постоянная длительность принимается обычно в моделях обслуживания вызовов УУ. Случайная длительность обслуживания задается функцией распределения:

,

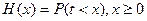где: t – длительность обслуживания вызовов.

Чаще всего используют отрицательное экспоненциальное распределение:

,

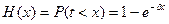где: 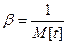- параметр длительности обслуживания.

Дифференцируя по (х), найдем плотность распределения вероятностей:

.

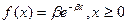Числовые характеристики распределения:

; ; .

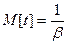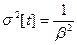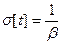1.8 Классификация потоков вызовов.

В ТТ рассматриваются две ветви классификации входящих потоков:

Ø Потоки с простым последействием;

Ø Потоки с ограниченным последействием;

Параметр потока с простым последействием зависит от состояния КС. Различают макросостояния КС и микросостояния КС

Под макросостояниями КС понимается наиболее общая характеристика состояния системы в момент времени (t). Например, общее число занятых входов, выходов ПЛ и т.д. Число таких состояний для однозвенных, ПД КС равно (v+1).

Под микросостояниями КС понимается детальная информация о состоянии системы в момент времени (t), т.е. не только общее число занятых входов, выходов, ПЛ, но и информация о том, какие именно входы, выходы, ПЛ заняты.

Число таких состояний для однозвенного, НД пучка емкостью v линий равно 2^v.

Под потоком с простым последействием понимается ординарный поток, для которого в любой момент времени (t) существует конечный параметр потока в состоянии (s), зависящий только от состояния (s) КС в момент времени (t) и не зависящий от процесса обслуживания вызовов до этого момента. Это ординарный, нестационарный поток. Обозначим его параметр - ^sl.

Частным случаем потока с простым последействием является симметричный поток.

Симметричным потоком называется поток с простым последействием, параметр которого в любой момент определяется числом обслуживающихся вызовов в этот момент времени и не зависит от других характеристик КС.

^sl=l_i,

где: i – число занятых линий.

Частным случаем симметричного потока является примитивный поток вызовов.

Примитивным потоком называется такой симметричный поток, параметр которого - l_i прямо пропорционален числу свободных в данный момент источников:

l_i=(n-i)a,

где: i – число занятых источников;

a - параметр потока одного свободного источника.

Частным случаем примитивного потока является простейший поток вызовов. Параметр l простейшего потока вообще не зависит от состояния КС и для данного потока является величиной постоянной.

Математической моделью простейшего потока является формула Пуассона:

,

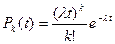а примитивного потока – формула Бернулли (t=1):

,

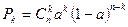где: n – общее число источников нагрузки,

а – удельная нагрузка от одного источника.

Частным случаем потока с простым последействием является также поток с повторными вызовами.

В этом потоке следует различать первичные и вторичные вызовы. В качестве первичного потока могут выступать либо простейший, либо примитивный потоки. В случае простейшего потока суммарный параметр входящего потока определяется следующим образом:

,

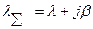где: l - параметр первичного потока вызовов,

j – число источников повторных вызовов (ИПВ),

b - параметр потока одного ИПВ.

Если поток первичных вызовов является примитивным, то:

,

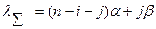где: n – общее число источников вызовов,

i – число занятых источников,

j – число ИПВ.

Вторая ветвь классификации потоков вызовов связана с функцией распределения промежутков между вызовами.

Наиболее общим видом потока в этой классификации является поток с ограниченным последействием.

Потоком с ограниченным последействием называется поток, у которого промежутки между вызовами взаимно независимы и имеют любые распределения.

.

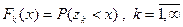Частным случаем потока с ограниченным последействием является рекуррентный поток.

Рекуррентный поток характеризуется одинаково распределенными промежутками между вызовами:

F₁(x)=F₂(x)=…=F(x).

Некоторым обобщением рекуррентного потока является рекуррентный поток с запаздыванием, для которого:

F₁(x)¹F₂(x)= F₃(x)=…=F(x).

Стационарный, ординарный, рекуррентный поток с запаздыванием называется потоком Пальма

Для потока Пальма, как и для любого стационарного ординарного потока:

.

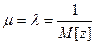Функция распределения первого промежутка между вызовами для потока Пальма определяется как

;

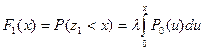Для остальных промежутков между вызовами:

,

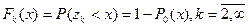где: Р₀(х) – вероятность отсутствия вызовов на интервале длиной (х).

Важной для практики является следующая теорема Пальма:

Если на КС с явными потерями и с показательным распределением длительности обслуживания поступает поток Пальма, то поток необслуженных (потерянных) вызовов также будет потоком Пальма.

Простейший поток вызовов является частным случаем потока Пальма, для которого все промежутки между вызовами (включая первый) имеют показательное распределение.

В отдельную группу выделяются потоки Эрланга, которые образуются с помощью рекуррентной операции просеивания. Смысл этой операции заключается в том, что очередной поступивший вызов с вероятностью r остается (просеивается), а с вероятностью (1-r) теряется. Новый поток называется просеянным.

Поток, полученный из рекуррентного с помощью операции просеивания, также будет рекуррентным.

Важным для практики является случай, когда операции просеивания подвергается простейший поток. В этом случае просеянный поток (имеет место на направлениях КС, работающей в режиме Г) будет также простейшим с параметром - lr.

Если (m) вызовов теряется, а (m+1) просеивается, то получим поток Эрланга m-го порядка. Например, сохраняя в простейшем потоке каждый 3-ий вызов, получаем поток Эрланга 2-го порядка и т.д.

Простейший поток можно рассматривать как поток Эрланга 0-го порядка.

Моменты распределения промежутков между вызовами потока Эрланга m-го порядка определяется следующими выражениями:

; ; .

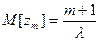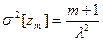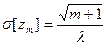Параметр этого потока:

.

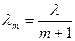Потоки Эрланга m-го порядка при разных (m) создают потоки с различной степенью случайности:

При (m=0) – простейший;

При (m=¥) – детерминированный.

В моделях обслуживания входящих потоков важное место занимает поток освобождений.

Под потоком освобождений понимается последовательность окончания обслуживания вызовов.

При обслуживании поступающего потока без потерь при постоянном времени обслуживания (h) свойства потока освобождений совпадают со свойствами входящего потока. Просто происходит сдвиг моментов на величину (h).

При обслуживании простейшего потока без потерь при показательном распределении времени обслуживания, поток освобождений будет также простейшим с параметром, равным числу занятых линий в КС:

,

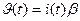где: i(t) – число занятых линий в момент (t);

b - параметр потока освобождений одной линии (постоянная обслуживания вызовов).

Дата добавления: 2014-01-11