Постановка задачи. Обслуживание симметричного потока вызовов

Обслуживание симметричного потока вызовов

Под симметричным потоком понимается поток с простым последействием, параметр которого в любой момент времени определяется числом занятых линий в коммутационной системе - .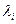

Дано: П – входящий поток симметричный с параметром - ;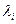

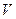- КС однозвенная полнодоступная;

D – дисциплина обслуживания с явными потерями;

- закон распределения промежутков между вызовами показательный;

- закон распределения времени обслуживания вызовов показательный.

Определить:

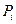- вероятность того, что в системе занято точно 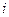линий в любой произвольный момент времени;

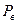- вероятность потерь по вызовам;

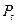- вероятность потерь по времени.

Решение

Обозначим на оси времени отрезок

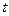
и на первом этапе решения задачи определим вероятности .

Возможные переходы системы за промежуток 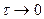сведены в таблицу 3.1.

Таблица 3.1 – Вероятности переходов

Момент	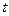Промеж.	Момент	Вероятность перехода
… … …	-

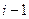
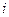
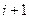
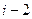
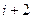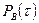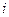
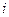
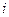
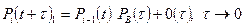
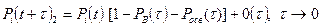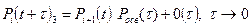
Величины 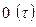в таблице учитывают вероятности неординарных переходов.

Очевидно, что

.

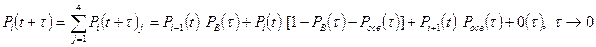Последнее выражение при разных 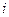принимает следующий вид

,

…

,

…

.

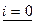
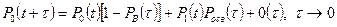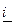
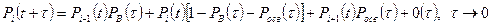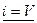
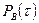Итак, получена система уравнений. Число уравнений в системе и неизвестны вероятности и . Найдем их.

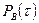определим, используя выражение для параметра потока

.

Тогда .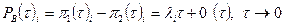

Величина прямо пропорциональна числу занятых выходов системы и длине промежутка (будет доказана ниже).

.

Перепишем систему уравнений с учетом полученных выражений

,

…

,

…

.

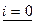
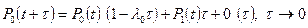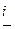
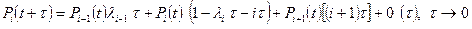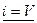
Решаем полученную систему уравнений. Для этого выполняем следующие операции:

- Раскрываем скобки;

- Произведение 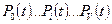на единицу переносим из правых частей в левые;

- Разделим обе части уравнений на ;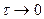

- Возьмем предел от обоих частей при .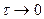

После выполнения указанных преобразований, устремляя , в левой части уравнений получаем

.

Тогда система уравнений принимает вид

,

…

,

…

.

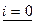
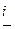
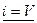
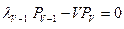Решаем систему уравнений. Из первого уравнения ,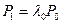

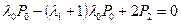. Откуда .

. .

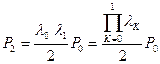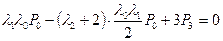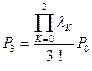Выдвигаем гипотезу о том, что решение системы в общем виде следующее

; .

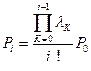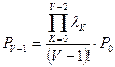Подставляя выражение для в последнее уравнение системы и разрешая его относительно имеем

, что подтверждает справедливость гипотезы.

В полученных выражениях неизвестна вероятность 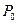. Для ее определения восиспользуемся условием нормировки.

.

Подставляя в последнее уравнение выражение для 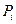, разрешаем его относительно 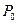, получаем

.

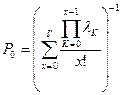Окончательно

.

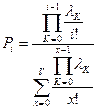Потери по времени

.

Определим потери по вызовам. Согласно определению 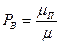(отношение интенсивностей потерянного к поступающему потокам вызовам).

; .

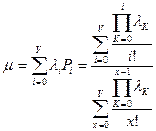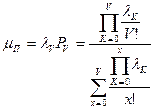Окончательно

.

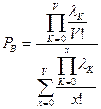Таким образом, определены величины:

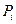- - вероятность занятости точно 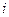линий в произвольный момент времени;

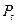- - потери по времени;

- - потери по вызовам.

Дата добавления: 2014-01-11