Однолинейный пучок. Формула Полячека-Хинчина

Модели M/M/1, М/D/1. Результаты Берка.

В системах автоматической коммутации особое место занимают частные случаи рассмотренных выше моделей при v=1.Такие модели обслуживания называются однолинейными.

Эти модели исследовали Полячек и Хинчин, которые независимо друг от друга получили выражение для среднего времени ожидания начала обслуживания при простейшем входящем потоке

,

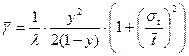где: l- параметр входящего потока;

y-нагрузка, поступающая на однолинейную систему (y<1);

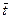- среднее время обслуживания одного вызова;

s_t- среднеквадратическое отклонение(СКО) времени обслуживания.

Наличие в приведенной формуле величины s_t указывает на ее универсальный характер, т.е. описывает модели М/М/1 и М/D/1.

Полагая 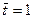, получаем

,

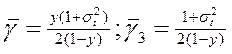где: s_t- СКО длительности обслуживания в условных единицах (t=1).

Тогда для системы М/М/1 при s_t=1

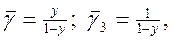
а для системы М/D/1 при s_t = 0:

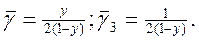
Таким образом, при постоянной длительности обслуживания среднее время ожидания для любого вызова -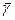и задержанного вызова - 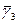вдвое меньше, чем при показательно распределенной длительности занятия.

Качественные показатели рассмотренных моделей зависят от дисциплины выбора вызова из очереди на обслуживание. Они могут быть следующими:

- в порядке поступления (в порядке очереди),

- в случайном порядке.

Этот вопрос исследовался английским ученым Берком. Результаты, полученные Берком, иллюстрируются кривыми на рис.4.8, где пунктирными кривыми представлена дисциплина выбора в порядке очереди, а сплошными кривыми в случайном порядке.

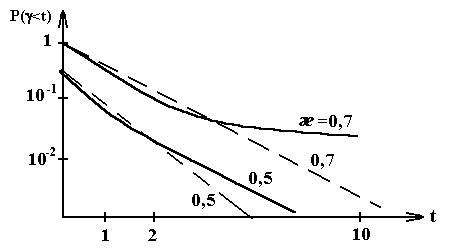
Рис. 4.8 – Кривые Бёрка.

Из рисунка видно, что в области небольших значений t показатели обслуживания выше при случайном порядке выбора, а в области больших t они меняются местами.

В заключении отметим, что случайный выбор вызовов из очереди на обслуживание наиболее полно описывает модели с малыми очередями(когда очереди нет вообще или она очень редко превышает единицу).

Результаты Берка нашли применение при расчете качественных показателей работы управляющих устройств (маркеров) в координатных системах АТС.

4.6 Область применения систем с ожиданием

и систем с потерями.

Детальное изучение систем с ожиданием и с потерями показывает, что одну из них можно с максимальным эффектом применять в одной области потерь, а другую в другой области потерь в частности в разговорных трактах системы с ожиданием не дали должного эффекта. Это объясняется тем, что T_р (среднее время чистого разговора) порядка120 с. Если использовать систему с ожиданием, то длительность установления соединения может зачастую превышать эту величину. Т.е. использование приборов будет плохим. Поэтому разговорный тракт строится с применением систем с явными потерями. В области потерь P£0,01¸0,02 целесообразно использовать системы с явными потерями, тем более, что они имеют большую пропускную способность.

Для управляющих устройств целесообразно использовать дисциплину обслуживания с ожиданием. Это объясняется тем, что среднее время занятия управляющего устройства одним соединением мало

t= (70¸90) С- среднее время обслуживания одного вызова.

t’=£1 С.- среднее время занятия управляющего устройства одним вызовом.

Проиллюстрируем эти положения на следующем примере.

Имеется пучок v=1 P(П)=0,3, а P(0)=0,4 y=0,4Эрл.

v=2, а y=1Эрл. тогда P(П)=0,2, а P(0)=0,25.

Средняя длительность одного обслуживания t=1с, а среднее время ожидания начала обслуживания t₀=(1.2¸1,5) с. абонент такое время не (1,2¸1,5)с не ощущает, зато потери 20% в системе с потерями довольно существенны.

Вывод: Там где имеется небольшой пучок и время обслуживания мало целесообразнее использовать систему с ожиданием. При этом системы с ожиданием позволят улучшить использование линий пучка и повысить качество обслуживания.

4.7. Вопросы для самоконтроля

ü Какое ограничение вводится на величину поступающей нагрузки в системах с ожиданием?

ü Напишите вторую формулу Эрланга. Что она определяет? От каких параметров зависит?

ü Какими формулами определяется среднее время ожидания начала обслуживания и средняя длина очереди?

ü В чем сущность теории Кроммелина? Чем она отличается от второй формулы Эрланга?

ü Какая модель обеспечивает более высокое качество обслуживания вызовов?

ü Приведите формулу Полячека-Хинчина.

ü Какой вид принимает формула Полячека-Хинчина для моделей М/М/1 и М/D/1?

ü Сравните время ожидания начала обслуживания при случайной выборки вызовов из очереди и в порядке поступления.

ü Укажите рациональную область применения систем с ожиданием и систем с явными потерями.

Дата добавления: 2014-01-11