Функция распределения времени ожидания начала обслуживания. Постоянная длительность занятия. Формула Кроммелина

Модель типа M/D/V.

В технике автоматической коммутации многие приборы имеют постоянную длительность обслуживания вызовов и дисциплину обслуживания с ожиданием. Примером являются маркёры. Обозначим буквой h среднюю длительность обслуживания вызова маркёром.

Постановка задачи: Имеется полнодоступный пучок линий с емкостью v, включенный в однозвенную коммутационную систему. На этот пучок поступает простейший поток вызовов с параметром l. Обслуживание каждого вызова осуществляется с постоянной длительностью h. Вызовы обслуживаются в порядке очереди, т.е. «пришел последним – обслуживается последним».

Определить: .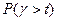

В нашем случае: 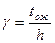- время ожидания начала обслуживания в относительных единицах.

t_ож – время ожидания начала обслуживания в относительных единицах. За единицу времени принимается длительность обслуживания одного вызова. Тогда заданное время ожидания в условных единицах определяется следующим образом:

.

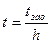Пусть в момент наблюдения система находится в состоянии «k», т.е. на обслуживании и на ожидании находится ровно «k» вызовов.

Вводим обозначения:

P_k – вероятность того, что система находится в состоянии «k».

a_k – вероятность того, что система находится в состоянии, не превышающем «k» (0, 1, 2, …, ¥).

Тогда

.

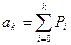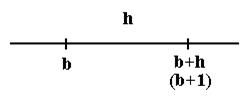
Рассмотрим состояние системы в два момента времени b и b+h, где h – длительность обслуживания одного вызова. Т.к. h=1 (мы приняли ее за единицу времени), то b+h=b+1. Если b+1, то всё в дальнейшем будем оценивать в условных (относительных) единицах.

Пусть в момент времени «b» все линии пучка заняты обслуживанием вызовов. Когда закончится обслуживание этих вызовов?

Наверняка эти вызовы будут обслужены до момента b+1, т.к. длительность обслуживания каждого вызова постоянна и равна h.

Рассмотрим состояние системы в момент «b» и «b+1».

В момент b+1(b+h) в системе должно быть k вызовов.

Если за время «h» освободилось v вызовов, то чтобы в момент b+1 было k вызовов за это время (h=1) должно поступить «k» вызовов. Эти k вызовов создаются простейшим потоком, для которого вероятность поступления k вызовов равна

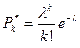- формула Пуассона (h=1) за единицу времени.

Тогда 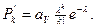здесь а_v учитывает то, что в момент “b” система находилась в состоянии меньше или равно v.

Если в момент»b» число вызовов было меньше чем (v+i). За h=1 будет v освобождений. Для того, чтобы в момент, «b+1» было k вызовов, за h должно поступить «k-i» вызовов.

Тогда по закону Пуассона имеем

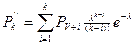
Сумма изменяется до «k», т.к. нас интересует, чтобы в момент «b+1» было всего k вызовов.

Отсюда 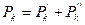. Вероятность того, что система будет находиться в состоянии «k»

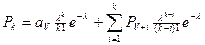
Нам необходимо определить P (g>t)-?

В начале определим величину P(g<t), а нужная величина определиться так P(g>t)=1-P(g<t).

Определим сколько вызовов будет обслужено за t единиц времени, если всегда на ожидании есть вызовы.

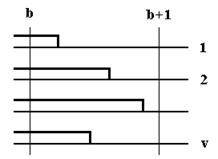В каждую единицу времени обслуживается v вызовов. Тогда за «t» единиц будет обслужено «tv» вызовов. Кроме этого на обслуживании находится «v» вызовов, т.к. есть вызовы, ждущие обслуживания. Следовательно всего вызовов будет

tv+v,

где: tv- обслужено до момента t₁;

v- нах. на обсл. в t₁;

Для «k+1» вызова должно выполняться условие k+1£ tv+v

При этом условии этот вызов будет ожидать обслуживания время g< t с вероятностью P(g<t)

Если в момент поступления вызова система была в состоянии k=tv+v-1, то поступивший вызов будет ожидать начала обслуживания в течение времени g<t.

Тогда

Перейдя к P(g>t) имеем

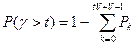- формула Кроммелина.

Им же было построено семейство кривых

P(g>t)= ¦(t) при v=1¸20 и æ=0,002¸0,8 эрл.

Характер этих кривых такой же, как и при экспоненциальной длительности обслуживания. Различие лишь в количественной стороне

P(g>t)=¦(t), æ = æ₁, v₁=1, v₂>1

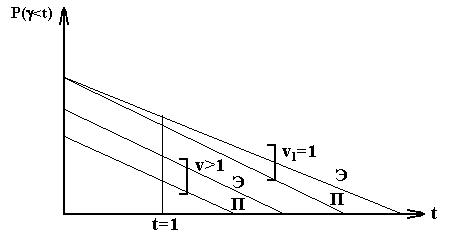
Рис. 4.7 - Зависимость P(g>t)= ¦(t) при v=v₁, v₂.

Здесь: П- постоянная длительность обслуживания.
Э- экспоненциальная длительность обслуживания

Из графика видно, что чем больше v тем ниже P(g>t), тем лучше качество обслуживания.

Постоянная длительность обслуживания обеспечивает лучшее качество обслуживания(большая пропускная способность).

При t=0, v=1 P(g>0)=P_t и потери не зависят от закона распределения длительности обслуживания.

Приведём примеры, иллюстрирующие эти графики:

v=1 æ=0,5, но æ 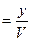, следовательно, y= 0,5.

	П	Э
P(g>0)	0,5	0,5
P(g>1)	0,17	0,25
P(g>2)	0,06	0,2
P(g>3)	0,012	0,15

P(g>1)=0.17. Это значит, что 17 вызовов из 100 будут ждать в течение времени g>1.

v=4 тогда y=æ×v=0,5×4=2эрл.

	П	Э
P(g>0)	0,15	0,25
P(g>1)	0,005	0,03
P(g>2)	0,0001	0,002

P(g>0)=P_t – вероятность того, что имеются вызовы на ожидании потери по времени).

Как уже отмечалось, постоянная длительность обслуживания реализуется в маркерном оборудовании.

Если маркер построен на релейной базе, то

h=(0,1¸1,2) c.

Если маркер выполнен на электронных элементах, то

h=(0,01¸0,2) c.

Пример: имеется АТС на 10000 номеров

С=3 вызовов в ЧНН (от одного источника нагрузки)

h=0,08 с (длительность обслуживания каждого вызова маркером).

Найдем нагрузку на маркер

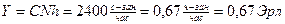
Нагрузка на маркер y<1 эрл. следовательно для ее обслуживания достаточно одного маркера. (v=1)

Примем допустимое время ожидания начала обслуживания в относительных единицах равным (6¸7)

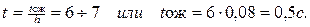
По кривым Кроммелина находим, что P(g>6)=0,01

В одном проценте случаев время ожидания начала обслуживания превысит 0,5с. Это для абонентов неощутимая задержка.

Дата добавления: 2014-01-11