Тема 4 полнодоступный пучок. Система с ожиданием

4.1 Постановка задачи.

Под системой с ожиданием понимается такая дисциплина обслуживания поступающего потока вызовов, когда поступивший вызов при занятости соединительных путей, способных его обслужить, не теряется, а становится в очередь и обслуживается с ожиданием.

Пусть имеется КС из v линий. При числе занятых линий 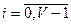поступающий поток вызовов обслуживается без ожидания. Когда i=v, то поступивший вызов становится в очередь и обслуживается с ожиданием.

Таким образом, при i£v-1 система с ожиданием не отличается от системы с потерями. При i=v вновь поступившие вызовы станут на ожидание, т.е. будут условно потеряны. Обозначим через «j» число вызовов, стоящих на ожидании.

Пример: Пусть входящий поток вызовов примитивный. Тогда j_макс=k-v – максимальная длина очереди. В случае простейшего потока «k» неограниченно и поэтому j=0, 1,..., ¥.

КС полнодоступная, поэтому любой вход доступен любому выходу. Следовательно, не нужно заниматься исследованием микросостояний КС, а достаточно ограничиться исследованием макросостояний (общее число занятых источников, а не их номера).

Для простейшего потока ^sl=l не зависит от состояния КС. Под состоянием КС будем понимать число занятых линий, а если заняты все, то число вызовов, находящихся на ожидании:

i – число занятых линий;

j – число вызовов на ожидании.

Здесь могут быть следующие случаи:

Ø В пучке занято точно i линий и i<v (i=0, 1, 2,...,v-1), то k=i. Число занятых линий при i<v однозначно определяет состояние КС. В этом случае может быть всего v состояний.

Ø i=v и на ожидании j=0, 1, 2,... вызовов, то k=v+j. В этом случае может быть ¥ число состояний. Таким образом, число макросостояний равно ¥.

В системах с потерями на величину нагрузки не накладывается никаких ограничений. При этом, чем больше нагрузка, тем больше были потери. В системах с ожиданием все вызовы должны быть обслужены. Поэтому во избежании очереди, равной ¥ на величину входящей нагрузки необходимо ввести ограничения. Какие? Допустим, что y<v. Каждая линия может обслужить максимально 1 Эрланг, следовательно, v линий – v Эрланг. При y=v все линии будут непрерывно заняты, а при y>v очередь будет стремиться к ¥; из-за неравномерности поступающих вызовов и при y=v длина очереди тоже будет стремиться к ¥.

Таким образом, обязательное условие:

y<v –

- вообще, а для простейшего потока вызовов: у=l<v.

4.2 Обслуживание однозвенной полнодоступной коммутационной системой простейшего потока вызовов. Система с ожиданием. Модель типа M/M/V. Вторая формула Эрланга

Имеется полнодоступная однозвенная коммутационная система с пучком емкостью v линий. На эту систему поступает простейший поток вызовов с параметром l. Закон распределения длительности обслуживания экспоненциальный:

H(x)=P(T<x)=1-e^-x.

Принимаем, как и раньше, что постоянная обслуживания b=1.

Какова вероятность того, что в системе занято точно i линий. P_i=?

Какова вероятность того, что на ожидании находятся ровно j вызовов. W_j=?

Кроме этого P_t=?, P_в=?

Все это при ограничении l<v.

Нас интересует в любой произвольный момент времени P_i(t), W_j(t). Рассмотрим вначале не момент времени t, а момент времени [t+t).

Все дальнейшие рассуждения будут проводиться при условии, что t®0. вероятности P_i и W_j определяются состоянием коммутационной системы.

Каковы эти состояния?

Момент времени t	За t
i-1	1 выз.
i	-
i +1	1осв.
j-1	1 выз.
j	-
j+1	1 осв.

Остальные состояния имеют место с вероятностью о(t).

Пока система находится в состоянии V=1, то обслуживание с ожиданием не отличается от обслуживания с потерями. Поэтому первые V-1 уравнений будут такими же как и раньше, т.е.

i=0: P₀(t+t)=P₀(t)[1-P_в(t)]+P₁(t)P_осв(t)+o(t);

в общем виде: P_i(t+t)=P_i-1(t)[P_в(t)]+P_i(t)[1-P_в(t)-P_осв(t)]+ P_i+1(t)P_осв(t)+o(t), t®0.

i=v: при i=v, j=0, 1, 2,..., ¥.

Обозначим через P_v(t+t) – вероятность того, что в системе занято v линий и на ожидании находятся 0 вызовов. Тогда P_v(t)=W₀(t) и

P_v(t+t)=W₀(t+t)=P_v-1(t)P_в(t)+P_v(t)[1-P_в(t)-P_осв(t)]+ +W₁(t)P_осв(t)+o(t), t®0.

Здесь W₁(t) – вероятность того, что на ожидании находится один вызов.

W_j(t+t) -? при i=v

W_j(t+t)=W_j-1(t)P_в(t)+W_j(t)[1-P_в(t)-P_осв(t)]+W_j+1(t)P_осв(t)+o(t), j=0, 1, 2,..., ¥; t®0.

При j=0 справедливо предыдущее уравнение.

Итак, мы имеем систему бесконечного числа уравнений. Неизвестно P_в(t)-? P_осв(t) -? Эти величины не зависят от дисциплины обслуживания, т.к. являются атрибутами потока вызовов. Поэтому можно воспользоваться ранее полученными выражениями:

P_в(t)=l_it+o(t), P_осв(t)=it+o(t)

или при l_i=l:

P_в(t)=lt+o(t), P_осв(t)=it+o(t).

i<v: P_осв(t)=it+o(t);

i=v; j=0, 1, 2,..., ¥: P_осв(t)=vt+o(t) при любом j;

P₀(t+t)=P₀(t)[1-lt+o₁(t)]+P₁(t)[t+o₂(t)]+o₃(t), t®0;

P_i(t+t)=P_i-1(t)[lt+o₁(t)]+P_i(t)[1-lt+o₂(t)-it+o₃(t)]+ +P_i+1(t)[(i+1)t+o₄(t)]+o₅(t), t®0, i=1, 2,..., v-1;

P_v(t+t)=P_v-1(t)[lt+o₁(t)]+P_v(t)[1-lt+o₂(t)-vt+o₃(t)]+o₄(t)+W₁(t)[vt+o₅(t)];

W_j(t+t)=W_j-1(t)[lt+o₁(t)]+W_j(t)1[1-lt+o₁(t)-vt+o₂(t)]+ +W_j+1(t)[vt+o₃(t)]+o₄(t), j=0, 1, 2,..., ¥; t®0.

Перенесем в левые части из правых P₀(t), P_i(t), W_j(t) и возьмем предел предварительно поделив все на t®0.

Тогда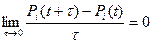

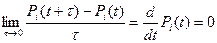
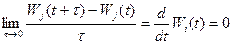
Производные по t равны нулю, т.к. поток стационарен и P_i(t)=P_i и W_j(t)=W_j.

В правой части все отношения 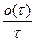в пределе равны нулю:

.

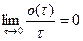С учетом вышеизложенных замечаний получим систему:

i=0: -lP₀+P₁=0;

i=1,..., v-1: lP_i-1-(l+i)P_i+P_i+1(i+1)=0;

i=v, j=0: lP_v-1-(l+v)P_v+vW₁=0;

i=v, j=1,..., ¥: lW_j-1-(l+v)W_j+vW_j+1=0.

Выразим P_i и W_j через P₀:

i=0: Р1=lР₀;

i=1: lP₀-(l+1)P₁+2P₂=0;

lP₀-(l+1)P_ol+2P₂=0;

l²P₀=2P₂;

;

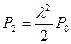i=2: lP_i-(l+2)P₂+3P₃=0;

;

;

.

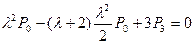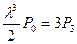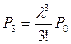С помощью метода индукции можно предположить, что эта закономерность верна для других i, т.е.

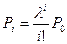
Проверим правильность этого утверждения для i=v.

v-1=i:

lP_v-2-(l+v-1)P_v-1+vP_v=0;

;

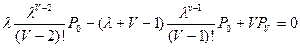После упрощений:

;

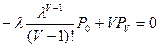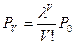
что и требовалось доказать. Таким образом:

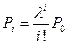, i=1,...,V-1;

.

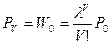Подставим эти выражения в уравнение для j=0.

j=0:

,

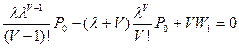откуда:

.

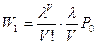j=1: Последнее уравнение системы:

,

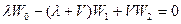откуда:

,

.

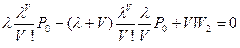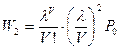Предположим, что этот закон справедлив для любого j:

.

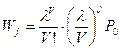Проверим справедливость гипотезы для W_j+1:

,

,

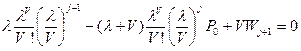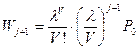что и требовалось доказать.

Найдем Р₀ из следующего условия:

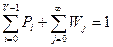, (I)

уравнение (I) можно записать иначе:

. (II)

Решим уравнение (I):

;

.

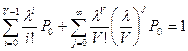Распишем вторую сумму в знаменателе:

.

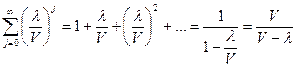l<v – ограничение, введенное при постановке задачи. Это бесконечно убывающая геометрическая прогрессия, ее сумма равна:

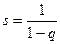при q<1,

где .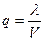

Для второго уравнения:

.

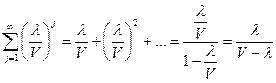Таким образом, для уравнения (I):

,

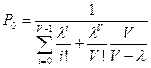Для уравнения (II):

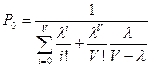
Подставим полученные выражения для P_i и W_j, а в знаменателе во избежание путаницы сменим переменные суммирования:

,

.

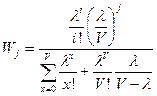Для простейшего потока вызовов l=у. Тогда:

.

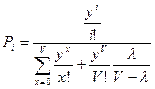Для простейшего потока было получено:

,

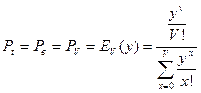а .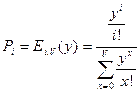

В выражении для P_i в системе с ожиданием произведем некоторые преобразования:

.

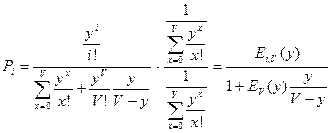Таким образом, для системы с ожиданием:

.

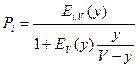Сравним P_i(П) и P_i(O),

где: P_i(П) – для систем с потерями,

P_i(O) – для систем с ожиданием.

В выражении для P_i(O) знаменатель больше 1. Следовательно:

Р_i(О)<Р_i(П).

Это в свою очередь означает:

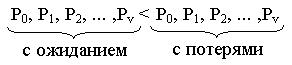
А это значит, что

.

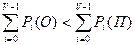Доля времени, в течение которой нет потерь, в системе с потерями больше, чем доля времени в системе с ожиданием.

Рекуррентная формула.

.

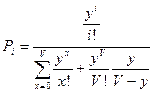Для i-1: .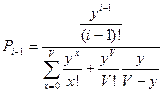

Найдем отношение.

,

.

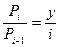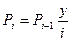
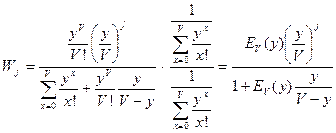Найдем рекуррентное соотношение.

;

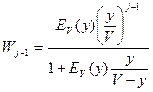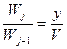
или

По условию y<v, поэтому 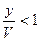, следовательно,

W_j < W_j-1 < W_j-2 <... илиW₀>W₁>W₂.

Определим потери по времени – P_t.

P_t – это доля времени, когда заняты все линии пучка и на ожидании может находиться j=0, 1, 2,..., ¥ вызовов.

.

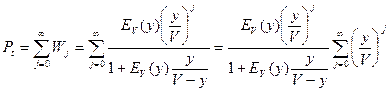Здесь 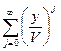сумма геометрической прогрессии .

.

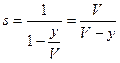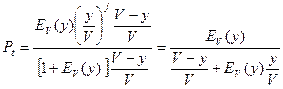Итак,

.

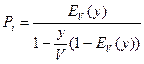Сравним P_t(П) и P_t(O). Знаменатель у P_t(O)<1, следовательно:

P_t(O)>P_t(П).

Потери по времени в системах с ожиданием больше потерь по времени в системах с потерями.

Найдем потери по вызовам.

.

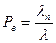В системах с ожиданием под потерями по вызовам понимается доля времени, в течение которой на ожидании находится хотя бы один вызов.

.

.

.

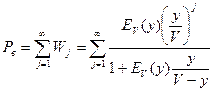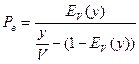Сравним Р_в(О) и Р_в(П).

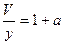, где 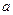- какое-то положительное число.

1-Е_v(у) – число также положительное.

Если 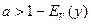, то знаменатель > 1.

Р_в(О)<Р_в(П)

Если , то

Р_в(О) 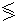Р_в(П)

Сравним для системы с ожиданием Р_t и Р_в.

; .

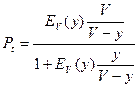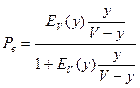, т.к. y<v, то 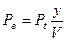, т.е.

Р_t>P_в.

Найдем Р_v:

,

,

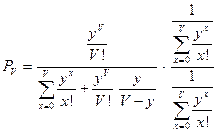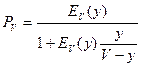откуда:

.

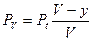Итак, мы получили: P_i, W_j, P_t, P_в ® f(y,v). Это вторая формула Эрланга. P_t – табулирована. Зная P_t можно найти P_v и Р_в. Проиллюстрируем полученные выражения графически.

y=f(v), при P=P₁, P₂.

При Р₁, v₁: y₁>y₂ , т.к. в системе с потерями пропускается большая нагрузка.

При у₁ в системе с «П» нужно v₁ линий, а в системе с ожиданием нужно v₂ линий.

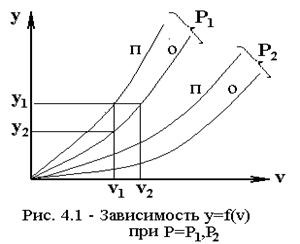v₂>v₁.

Пример: y=40 Эрл. и р=0,005:

v₁(П)=56 линий, v₂=60 линий.

Пропускная способность систем с потерями выше пропускной способности систем с ожиданием.

æ=f(v), при P=P₁, P₂.

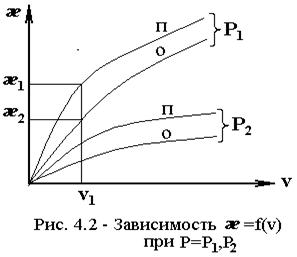
При v=v₁: æ₁>æ₂.

h=f(P), при v=v₁.

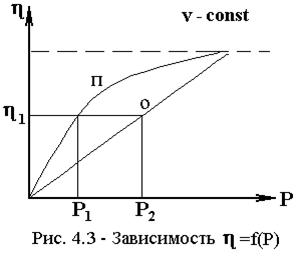В области малых потерь пропускная способность каждой линии пучка в системе с потерями выше, чем в системе с ожиданием. С увеличением потерь это отличие уменьшается.

Пример.

h=0,4 Эрл. v=10.

Р₁=4,5‰ Р₂=8‰

4.3 Функция распределения времени ожидания начала обслуживания. Экспоненциальное распределение длительности обслуживания вызовов.

В системах с ожиданием важно знать, сколько абонент будет ждать начала обслуживания. Здесь необходимо кроме P_t и Р_в найти t_ож (время ожидания начала обслуживания). В теории телетрафика t_ож характеризуют в вероятностном смысле следующей величиной:

P(t_ож<c) –

-это вероятность того, что время ожидания меньше какой-то «с». При этом, чем больше P(t_ож<c), тем лучше качество обслуживания и, наоборот, P(t_ож>c), тем хуже качество обслуживания.

Оценку лучше делать применительно к относительным величинам. За относительную единицу принимают среднее время обслуживания одного вызова (математическое ожидание) – МТ.

,

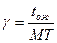где: g - время ожидания начала обслуживания одного вызова в условных единицах.

Найдем допустимое время ожидания начала обслуживания в относительных единицах.

,

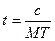где: с – допустимое время начала обслуживания в абсолютных единицах.

Какова же вероятность Р(g>t) при t=t₁,t₂,t₃?

Задача. На полнодоступный пучок линий емкостью v поступает простейший поток вызовов, создающий нагрузку у. Закон распределения длительности обслуживания экспоненциальный.

.

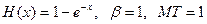Пусть l=y<v. Вызовы, находящиеся на ожидании обслуживаются в порядке очереди.

Требуется определить Р(g>t), т.е. вероятность того, что время до начала обслуживания превысит t.

Введем следующие обозначения:

1. k – состояние коммутационной системы. Общее число вызовов на обслуживание и ожидание. Если i=0¸v-1, то k=i. Если заняты все v линий пучка и j=0,1,…, то k=v+j.

2. P_k(g>t) – вероятность того, что вызов, поступивший в момент k-го состояния КС будет ждать начала обслуживания время, большее t.

3. Р_k – вероятность того, что система находится в k-ом состоянии (k=v+j).

Тогда

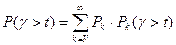
и есть вероятность того, что длительность ожидания начала обслуживания превысит

.

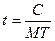При k=v+j очевидно следующее равенство:

P_k=W_j.

Тогда j=k-v и, следовательно, P_k=W_k-v. Величину W_k-v мы определили раньше. Тогда

.

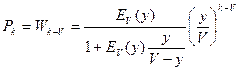Итак, в системе находится k вызовов всего, а на ожидании находится k-v вызовов. Положим, поступает k+1 вызов. Тогда он будет по очереди (k-v+1)-ым. Если за время t поступает k-v+1 вызов и все будут обслужены, то, очевидно, что выражение будет неправильным (время ожидания начала обслуживания ни у одного вызова не превысило t).

Чтобы это неравенство (g>t) было справедливо, необходимо, чтобы за время t было обслужено не более (k-v) вызовов. Тогда для k-v+1 вызова будет справедливым (g>t).

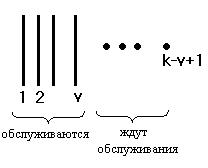Для этого необходимо, чтобы за время t было 1, 2, 3,…, k-v-2, k-v-1, k-v освобождений. Другими словами поток освобождений должен быть не более k-v. По условию, закон распределения длительности обслуживания экспоненциальный:

.

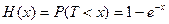Здесь Т – время обслуживания. Нас же интересует величина t в неравенстве g>t. В предыдущее выражение вместо (х) подставим (t):

или —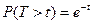

— это вероятность того, что длительность обслуживания превысит t. Эта величина для всех v линий равна:

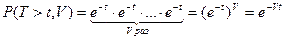
Тогда вероятность того, что хотя бы один из вызовов будет обслужен за время (T<t) будет равна:

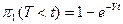
является характеристикой потока освобождений.

Функция распределения промежутков между вызовами для простейшего потока F(t) равна:

.

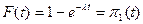Итак, поток освобождений есть простейший поток с параметром

l=v.

Для простейшего потока вероятность поступления за t равно i вызовов или i освобождений определяется формулой Пуассона:

,

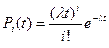при l=v: .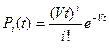

Тогда вероятность того, что за время t произойдет не более k-v освобождений есть сумма:

.

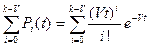А это, как было показано выше, и есть вероятность P_k(g>t):

.

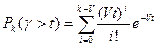Подставляем выражения для P_k и P_k(g>t) в искомую формулу:

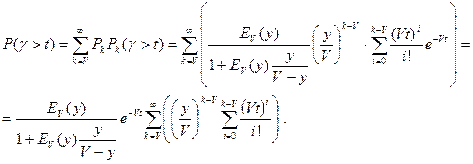
Рассмотрим эти выражения и упростим их.

1.

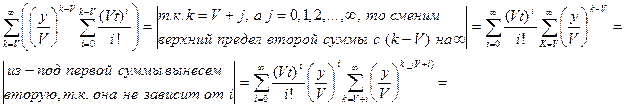
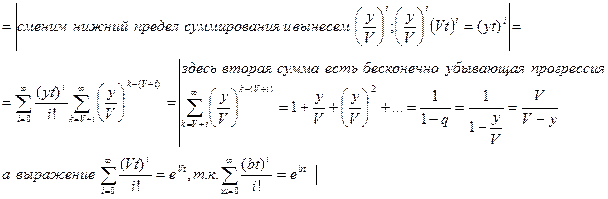
С учетом этих преобразований:

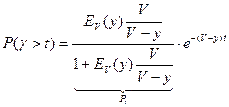
или .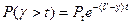

Таким образом, P(g>t)=f(t,y,v). Для разных t эта формула табулирована.

Системы с ожиданием характеризует более обще, чем g, ее средняя величина. Таким образом, 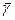- среднее время ожидания начала обслуживания (математическое ожидание начала обслуживания).

.

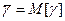Для непрерывной с.в., какой является время:

.

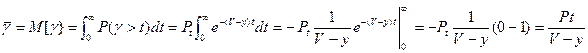
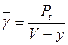Зная Р_t легко находится среднее время ожидания начала обслуживания. Р_t – табулирована. Кроме этой величины очень важно знать среднее число вызовов, находящихся на ожидании - 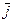. Аналогично с 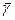--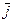 это математическое ожидании.

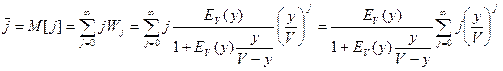
Найдем сумму :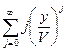

Тогда:

,

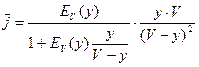Но

.

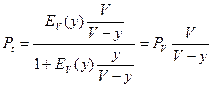Тогда

или .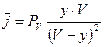

P_v – табулирована. Поэтому, зная ее, всегда можно найти и .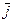

Итак, задача решена. Мы получили закономерности:

P(g>t) – вероятность того, что длительность ожидания начала обслуживания превысит t;

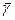- среднее время ожидания начала обслуживания;

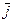- среднюю длину очереди.

Выражения для 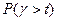, 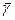и j, полученные выше есть функции от t, y, v, т.е

.

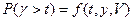Проиллюстрируем эти выражения на следующих графиках.

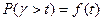при v=v₁, v₂, v₃,. причем v_1>v₂> v₃. Из графиков видно, что чем больше заданное время ожидания начала обслуживания, тем меньше вероятность .

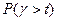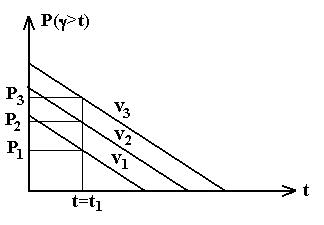
Рис. 4.4 – Зависимость 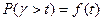при v=v₁, v₂, v₃.

Чем больше v, тем меньше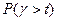, т.е. тем лучше качество обслуживания при заданном t. При фиксированном t=t₁:

.

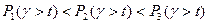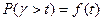, v=v₁, æ= æ₁, æ₂, æ₃ (пропускная способность).

æ₁< æ₂< æ₃.

При одной и той же емкости пучка с увеличением удельной пропускной способности 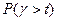увеличивается, т.е. ухудшается качество обслуживания.

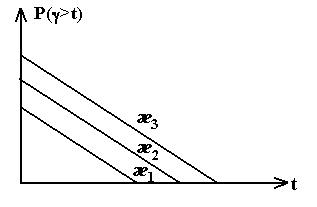
Рис. 4.5 – Зависимость 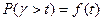при æ= æ₁, æ₂, æ₃.

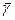=f(æ), v=v₁, v₂, v₃.

v₁<v₂<v₃.

Увеличение v при æ= æ₁ уменьшает среднее время ожидания начала обслуживания, т.е. качество обслуживания повышается.

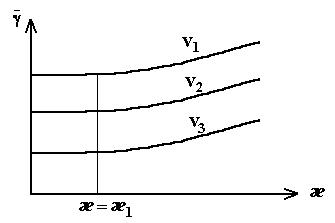
Рис. 4.6 – Зависимость 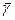=f(æ) при v=v₁, v₂, v₃.

Дата добавления: 2014-01-11