Распределенных систем обработки информации

Характеристик качества обслуживания

Приближенный метод расчета

Как уже отмечалось, исследуемые модели характеризуются тем, что в сети связи циркулируют потоки трафика, включающие информацию разного вида. При этом одни и те же ресурсы сети служат для коммутации и передачи потоков с отличающимися характеристиками, т.е. в данном случае имеет место многоканальная коммутация.

Объектом исследования в данном методе [18] авторы выбрали полнодоступную группу из v цифровых каналов. Входящим потоком принимается неординарный маркированный пуассоновский поток (НМПП). Общий поток интенсивностью m создается вызовами (n) типов, при этом каждый вызов с вероятностью 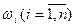требует одновременного наличия m_i свободных каналов, которые занимаются в течение времени h_i и после этого одновременно освобождаются.

Основная идея метода заключается в замене НМПП эквивалентным по действию ординарным рекуррентным потоком. Для обоснования данного подхода рассмотрим полнодоступную систему s, состоящую из v каналов. На систему поступает простейший поток с параметром l, причем каждый вызов требует для обслуживания m каналов и занимает их на время h. Моменты распределения поступающей нагрузки определяется как

; ,

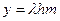а коэффициент скученности нагрузки

.

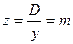Для расчета вероятности потери вызова исследуем модифицированную модель из 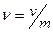комплектов, каждый из которых объединяет m каналов. Отдельно поступающему вызову требуется для обслуживания один из таких комплектов, поэтому поток вызовов можно считать ординарным. Поступающая нагрузка в модифицированной модели определяется числом занятых комплектов, считается пуассоновской первого рода с первым моментом, равным m×рр

h. Это положение позволяет определить вероятность потери вызова (p) по первой формуле Эрланга

.

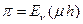В целом для системы s имеем:

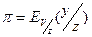, (7.1)

где: z – коэффициент скученности нагрузки.

В случае многомерных потоков нагрузки с заявками разных типов имеем:

; ,

где: .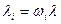

Откуда видно, что скученность суммарного потока неоднородных вызовов равна средневзвешенному числу каналов (m_i), которые требуются для обслуживания одной заявки i-го типа, с весами l_i×h_i×m_i, равным соответствующим нагрузкам.

После определения по формуле (7.1) средней вероятности потерь для произвольной заявки (p) расчет индивидуальных потерь (p_i) для заявок i-го типа (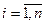) можно произвести с помощью приближенной формулы

. (7.2)

В таблице 7.1 приведены результаты расчета потерь по приведенным выше формулам и точным при n=3, m=3 и v=70.

Таблица 7.1 Результаты вычислений.

n	v	i	lihimi	mi	pi
прибл.	точно
					0,01347	0,0137
			0,0274	0,0293
			0,0412	0,0470

Из таблицы видно, что точность приближенной оценки вероятности потерь для индивидуальных потоков является вполне удовлетворительной.

Дата добавления: 2014-01-11