Ранговая корреляция

Пусть объекты генеральной совокупности обладают двумя качественными признаками (то есть признаками, которые невозможно измерить точно, но которые позволяют сравнивать объекты между собой и располагать их в порядке убывания или возрастания качества). Договоримся для определенности располагать объекты в порядке ухудшения качества.

Пусть выборка объема п содержит независимые объекты, обладающие двумя качествен-ными признаками: А и В. Требуется выяснить степень их связи между собой, то есть установить наличие или отсутствие ранговой корреляции.

Расположим объекты выборки в порядке ухудшения качества по признаку А, предполагая, что все они имеют различное качество по обоим признакам. Назовем место, занимаемое в этом ряду некоторым объектом, его рангом х_i: х ₁ = 1, х ₂ = 2,…, х_п = п.

Теперь расположим объекты в порядке ухудшения качества по признаку В, присвоив им ранги у_i, где номер i равен порядковому номеру объекта по признаку А, а само значение ранга равно порядковому номеру объекта по признаку В. Таким образом, получены две последовательности рангов:

по признаку А … х ₁, х ₂,…, х_п

по признаку В … у ₁, у ₂,…, у_п.

При этом, если, например, у ₃ = 6, то это означает, что данный объект занимает в ряду по признаку А третье место, а в ряду по признаку В – шестое.

Сравним полученные последовательности рангов.

1. Если x_i = y_i при всех значениях i, то ухудшение качества по признаку А влечет за собой ухудшение качества по признаку В, то есть имеется «полная ранговая зависимость».
2. Если ранги противоположны, то есть х ₁ = 1, у ₁ = п; х ₂ = 2, у ₂ = п – 1;…, х_п = п, у_п = 1, то признаки тоже связаны: ухудшение качества по одному из них приводит к улучшению качества по другому («противоположная зависимость»).
3. На практике чаще всего встречается промежуточный случай, когда ряд у_i не монотонен. Для оценки связи между признаками будем считать ранги х ₁, х ₂,…, х_п возможными значениями случайной величины Х, а у ₁, у ₂,…, у_п – возможными значениями случайной величины Y. Теперь можно исследовать связь между Х и Y, вычислив для них выборочный коэффициент корреляции

, (21.2)

где 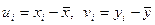(условные варианты). Поскольку каждому рангу x_i соответствует только одно значение y_i, то частота любой пары условных вариант с одинаковыми индексами равна 1, а с разными индексами – нулю. Кроме того, из выбора условных вариант следует, что 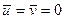, поэтому формула (21.2) приобретает более простой вид:

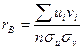. (21.3)

Итак, требуется найт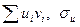и и .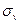

Можно показать, что 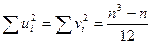. Учитывая, что 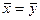, можно выразить 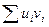через разности рангов 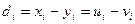. После преобразований получим: 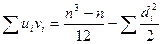, , 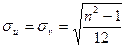откуда 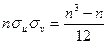. Подставив эти результаты в (21.3), получим выборочный коэффициент ранговой корреляции Спирмена:

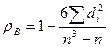. (21.4)

Свойства выборочного коэффициента корреляции Спирмена.

1. Если между А и В имеется «полная прямая зависимость», то есть ранги совпадают при всех i, то ρ_В = 1. Действительно, при этом d_i = 0, и из формулы (21.4) следует справедливость свойства 1.
2. Если между А и В имеется «противоположная зависимость», то ρ_В = - 1. В этом случае, преобразуя d_i = (2 i – 1) – n, найдем, что 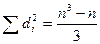, тогда из (21.4)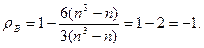
3. В остальных случаях -1 < ρ_B < 1, причем зависимость между А и В тем меньше, чем ближе | ρ_B | к нулю.

Итак, требуется при заданном уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена ρ_г при конку-рирующей гипотезе Н ₁: ρ _г ≠ 0. Для этого найдем критическую точку:

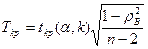, (21.5)

где п – объем выборки, ρ_В – выборочный коэффициент ранговой корреляции Спирмена, t_кр (α, k) – критическая точка двусторонней критической области, найденная по таблице критических точек распределения Стьюдента, число степеней свободы k = n – 2.

Тогда, если | ρ_B | < T_кр, то нулевая гипотеза принимается, то есть ранговая корреляционная связь между признаками незначима.

Если | ρ_B | > T_кр, то нулевая гипотеза отвергается, и между признаками существует значимая ранговая корреляционная связь.

Можно использовать и другой коэффициент – коэффициент ранговой корреляции Кендалла. Рассмотрим ряд рангов у ₁, у ₂,…, у_п, введенный так же, как и ранее, и зададим величины R_i следующим образом: пусть правее у ₁ имеется R ₁ рангов, больших у ₁; правее у ₂ – R ₂ рангов, больших у ₂ и т.д. Тогда, если обозначить R =R ₁ + R ₂ +…+ R_{n- 1}, то выборочный коэффициент ранговой корреляции Кендалла определяется формулой

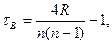(21.6)

где п – объем выборки.

Замечание. Легко убедиться, что коэффициент Кендалла обладает теми же свойствами, что и коэффициент Спирмена.

Для проверки нулевой гипотезы Н ₀: τ_г = 0 (генеральный коэффициент ранговой корреляции Кендалла равен нулю) при альтернативной гипотезе Н ₁: τ_г ≠ 0 необходимо найти критическую точку:

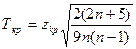, (21.7)

где п – объем выборки, а z_кр – критическая точка двусторонней критической области, определяемая из условия 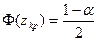по таблицам для функции Лапласа.

Если | τ_B | < T_кр, то нулевая гипотеза принимается (ранговая корреляционная связь между признаками незначима).

Если | τ_B | > T_кр, то нулевая гипотеза отвергается (между признаками существует значимая ранговая корреляционная связь).

Дата добавления: 2014-01-11