Регрессионный анализ. Рассмотрим выборку двумерной случайной величины (Х, Y)

Лекция 22.

Рассмотрим выборку двумерной случайной величины (Х, Y). Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним 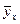назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее 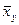- среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. В лекции 11 были выведены уравнения регрессии Y на Х и Х на Y:

M (Y / x) = f (x), M (X / y) = φ (y).

Условные средние 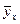и 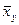являются оценками условных математических ожиданий и, следовательно, тоже функциями от х и у, то есть

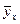= f* (x) - (22.1)

- выборочное уравнение регрессии Y на Х,

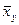= φ * (у) - (22.2)

- выборочное уравнение регрессии Х на Y.

Соответственно функции f* (x) и φ* (у) называются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если сам вид этих уравнений известен.

Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х ₁, у ₁), (х ₂, у ₂),…, (х_п, у_п). Будем искать параметры прямой линии среднеквадратической регрессии Y на Х вида

Y = ρ_yxx + b, (22.3)

Подбирая параметры ρ_ух и b так, чтобы точки на плоскости с координатами (х ₁, у ₁), (х ₂, у ₂), …, (х_п, у_п) лежали как можно ближе к прямой (22.3). Используем для этого метод наименьших квадратов и найдем минимум функции

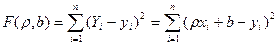. (22.4)

Приравняем нулю соответствующие частные производные:

.

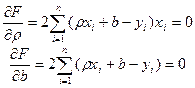В результате получим систему двух линейных уравнений относительно ρ и b:

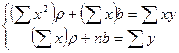. (22.5)

Ее решение позволяет найти искомые параметры в виде:

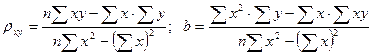. (22.6)

При этом предполагалось, что все значения Х и Y наблюдались по одному разу.

Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы:

Y	X
x 1	x 2	…	xk	ny
y1 y 2 … ym	n 11 n 12 … n 1 m	n 21 n 22 … n 2 m	… … … …	nk 1 nk 2 … nkm	n 11+ n 21+…+ nk 1 n 12+ n 22+…+ nk 2 …………….. n 1 m +n 2 m +…+ nkm
nx	n 11+ n 12+…+ n 1 m	n 21+ n 22+…+ n 2 m	…	nk 1+ nk 2+…+ nkm	n= ∑ nx = ∑ ny

Здесь n_ij – число появлений в выборке пары чисел (x_i, y_j).

Поскольку 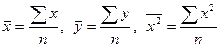, заменим в системе (22.5)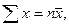

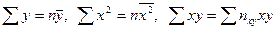, где п_ху – число появлений пары чисел (х, у). Тогда система (22.5) примет вид:

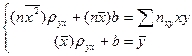. (22.7)

Можно решить эту систему и найти параметры ρ_ух и b, определяющие выборочное уравнение прямой линии регрессии:

.

Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы (22.7):

.

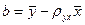Подставим это выражение в уравнение регрессии: 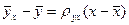. Из (22.7)

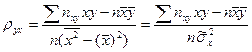, (22.8)

где 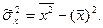Введем понятие выборочного коэффициента корреляции

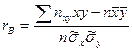
и умножим равенство (22.8) на 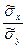: 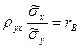, откуда 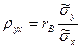. Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида

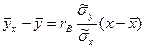. (22.9)

Дата добавления: 2014-01-11