Однофакторный дисперсионный анализ

Лекция 23.

Пусть генеральные совокупности Х ₁, Х ₂,…, Х_р распределены нормально и имеют одинаковую дисперсию, значение которой неизвестно. Найдем выборочные средние по выборкам из этих генеральных совокупностей и проверим при заданном уровне значимо-сти нулевую гипотезу Н ₀: М (Х ₁) = М (Х ₂) = … = М (Х_р) о равенстве всех математических ожиданий. Для решения этой задачи применяется метод, основанный на сравнении дисперсий и названный поэтому дисперсионным анализом.

Будем считать, что на случайную величину Х воздействует некоторый качественный фактор F, имеющий р уровней: F ₁, F ₂, …, F_p. Требуется сравнить «факторную дисперсию», то есть рассеяние, порождаемое изменением уровня фактора, и «остаточную дисперсию», обусловленную случайными причинами. Если их различие значимо, то фактор существенно влияет на Х и при изменении его уровня групповые средние различаются значимо.

Будем считать, что количество наблюдений на каждом уровне фактора одинаково и равно q. Оформим результаты наблюдений в виде таблицы:

Номер испытания	Уровни фактора Fj
F 1	F 2	…	Fp
… q	x 11 x 21 … xq 1	x 12 x 22 … xq 2	… … … …	x 1 p x 2 p … xqp
Групповое среднее			…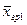

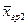
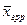
Определим общую, факторную и остаточную суммы квадратов отклонений от среднего:

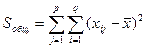- (23.1)

- общая сумма квадратов отклонений наблюдаемых значений от общего среднего ;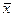

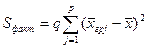- (23.2)

- факторная сумма отклонений групповых средних от общей средней, характеризующая рассеяние между группами;

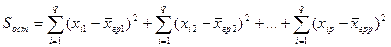- (23.3)

- остаточная сумма квадратов отклонений наблюдаемых значений группы от своего группового среднего, характеризующая рассеяние внутри групп.

Замечание. Остаточную сумму можно найти из равенства

S _ост = S _общ – S _факт.

Вводя обозначения 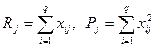, получим формулы, более удобные для расчетов:

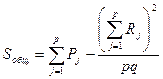, (23.1`)

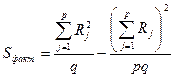. (23.2`)

Разделив суммы квадратов на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии:

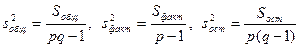. (23.4)

Если справедлива гипотеза Н ₀, то все эти дисперсии являются несмещенными оценками генеральной дисперсии. Покажем, что проверка нулевой гипотезы сводится к сравнению факторной и остаточной дисперсии по критерию Фишера-Снедекора (см. лекцию 12).

1. Пусть гипотеза Н ₀ правильна. Тогда факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии и, следовательно, различаются незначимо. Поэтому результат оценки по критерию Фишера-Снедекора F покажет, что нулевая гипотеза принимается. Таким образом, если верна гипотеза о равенстве математических ожиданий генеральных совокупностей, то верна и гипотеза о равенстве факторной и остаточной дисперсий.

2. Если нулевая гипотеза неверна, то с возрастанием расхождения между математичес-кими ожиданиями увеличивается и факторная дисперсия, а вместе с ней и отношение 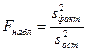. Поэтому в результате F _набл окажется больше F _кр, и гипотеза о равенстве дисперсий будет отвергнута. Следовательно, если гипотеза о равенстве математических ожиданий генеральных совокупностей ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.

Итак, метод дисперсионного анализа состоит в проверке по критерию F нулевой гипотезы о равенстве факторной и остаточной дисперсий.

Замечание. Если факторная дисперсия окажется меньше остаточной, то гипотеза о равенстве математических ожиданий генеральных совокупностей верна. При этом нет необходимости использовать критерий F.

Если число испытаний на разных уровнях различно (q ₁ испытаний на уровне F ₁, q ₂ – на уровне F ₂ , …, q_р - на уровне F _р), то

,

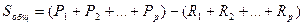где 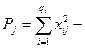сумма квадратов наблюдавшихся значений признака на уровне F_j,

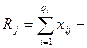сумма наблюдавшихся значений признака на уровне F_j. При этом объем выборки, или общее число испытаний, равен .

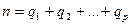Факторная сумма квадратов отклонений вычисляется по формуле

.

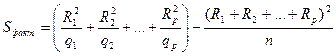Остальные вычисления проводятся так же, как в случае одинакового числа испытаний:

.

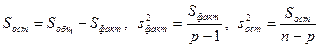Дата добавления: 2014-01-11