Приведение квадратичной формы к каноническому виду

Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.

Лекция 10.

Определение 10.1. Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

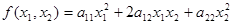(n = 2),

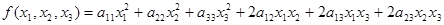(n = 3). (10.1)

Напомним данное в прошлой лекции определение симметрической матрицы:

Определение 10.2. Квадратная матрица называется симметрической, если , то есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

1) Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

Пусть матрица А имеет вид: . Составим характеристическое уравнение:

(10.2) Найдем дискриминант:

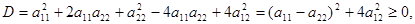следовательно, уравнение имеет только действительные корни.

2) Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

Координаты собственных векторов 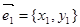и должны удовлетворять уравнениям:

Следовательно, их можно задать так:

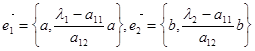. Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (10.2) получим, что Подставим эти соотношения в предыдущее равенство: 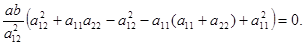Значит, .

Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

Определение 10.3. Матрицей квадратичной формы (10.1) называется симметрическая матрица 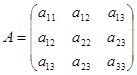. (10.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

Определение 10.4. Каноническим видом квадратичной формы (10.1) называется следующий вид: . (10.4)

Покажем, что в базисе из собственных векторов квадратичная форма (10.1) примет канонический вид. Пусть

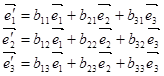- нормированные собственные векторы, соответствующие собственным числам λ₁,λ₂,λ₃ матрицы (10.3) в ортонормированном базисе . Тогда матрицей перехода от старого базиса к новому будет матрица

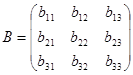. В новом базисе матрица А примет диагональный вид (9.7) (по свойству собственных векторов). Таким образом, преобразовав координаты по формулам:

,

получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам λ₁, λ₂, λ₃:

. (10.5)

Замечание 1. С геометрической точки зрения рассмотренное преобразование координат представляет собой поворот координатной системы, совмещающий старые оси координат с новыми.

Замечание 2. Если какие-либо собственные числа матрицы (10.3) совпадают, к соответствующим им ортонормированным собственным векторам можно добавить единичный вектор, ортогональный каждому из них, и построить таким образом базис, в котором квадратичная форма примет канонический вид.

Пример.

Приведем к каноническому виду квадратичную форму

x ² + 5 y ² + z ² + 2 xy + 6 xz + 2 yz.

Ее матрица имеет вид 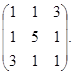В примере, рассмотренном в лекции 9, найдены собственные числа и ортонормированные собственные векторы этой матрицы:

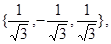
Составим матрицу перехода к базису из этих векторов:

(порядок векторов изменен, чтобы они образовали правую тройку). Преобразуем координаты по формулам:

^. Получим:

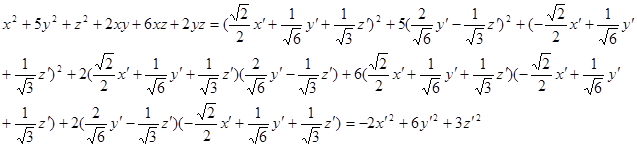Итак, квадратичная форма приведена к каноническому виду с коэффициентами, равными собственным числам матрицы квадратичной формы.

Дата добавления: 2014-01-11